O skinning de mesh é uma forma de deformar a mesh utilizando uma estrutura simples.
Para aplicações de tempo real, geralmente utilizamos a hierarquia de transformações.

1 Revisão Sobre Hierarquia de Transformações
A hierarquia de transformação é uma estrutura de dados de árvore que organiza a relação pai → filho de um conjunto de transformações.
Um exemplo pode ser visto na imagem a seguir:
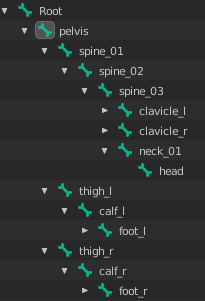
Existem diversos tipos de transformações, mas estamos interessados nos mais comuns: Translação, Rotação e Escala.
Nós usamos essas transformações combinadas para posicionar, rotacionar e escalar objetos 3D na cena virtual.
No passado, uma transformação era definida por mais de uma estrutura:
- Uma estrutura para representar rotações e escala: Se pensarmos em 2D, então precisamos de uma matriz de dimensão 2x2. Da mesma forma, para 3D, precisamos de uma matriz de dimensão 3x3.
- Outra estrutura para representar posições: em 2D temos um vetor [x,y], ou 3D, temos um vetor [x,y,z].
Para tornar possível utilizar uma estrutura única, utilizamos a coordenada homogênea.
Com a coordenada homogênea nós adicionamos uma nova linha à matriz onde 0 significa que a estrutura é um vetor e 1 significa que a estrutura é um ponto.
Com essa representação podemos definir nossa transformação com apenas uma matriz.
O interessante dessa representação é que quando multiplicamos uma matriz por um vetor, ela modifica a escala e rotação do vetor. Por outro lado, quando multiplicamos por um ponto, ela modifica a posição, escala e rotação do ponto.
Assim torna-se fácil criar composições mais complexas com as matrizes para criar nossa transformação.
Quando definimos uma hierarquia de transformações, nós queremos que os nós pais afetem os nós filhos.
Podemos implementar essa relação utilizando simples multiplicações de matrizes. Uma transformação é um termo genérico, mas pode ser encontrada com outros nomes, dependendo da aplicação. Por exemplo: juntas, bones, etc…
A imagem a seguir mostra como fazemos para calcular a transformação final de cada elemento na nossa hierarquia utilizando multiplicação de matrizes:
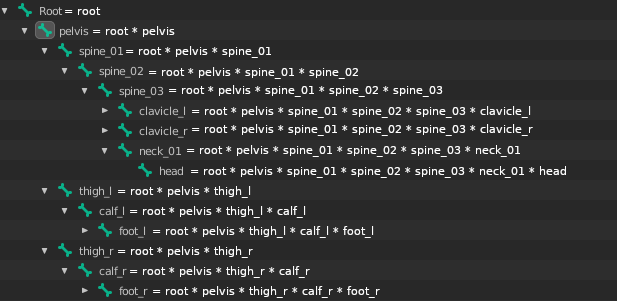
1.1 Raio-X da Matriz
Se você quer se aprofundar mais sobre transformações de matrizes, eu sugiro dar uma olhada em qualquer livro de computação gráfica clássica.
A representação de matriz que usaremos é orientada a coluna. Isso quer dizer que cada coluna dentro da matriz é nossa estrutura base (vetor ou ponto).
Veja o exemplo a seguir:
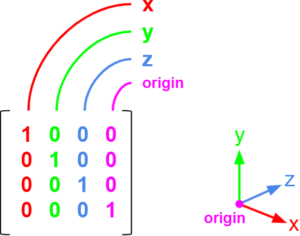
Cada coluna é um elemento no espaço 3D como você pode ver no gizmo no lado direito.
2 A Matriz Gradiente
A chave para entender a matemática por trás do skinning de mesh é entender a matriz gradiente.
2.1 Pontos e Vetores
Vou começar dando um exemplo com pontos e vetores.
Se nós temos 2 pontos e queremos representar uma operação que transforma o ponto ‘a’ no ponto ‘b’, podemos calcular o vetor ‘ab’.
Agora não precisamos armazenar o ponto ‘b’, porque podemos calculá-lo a partir do ponto ‘a’ somado ao vetor ‘ab’.
Veja a imagem a seguir:

2.2 Matriz de Transformação
Voltando com nossa matriz de transformação.
Como no exemplo que dei anteriormente com vetores e pontos, podemos fazer operações similares, mas agora utilizando multiplicações de matrizes.
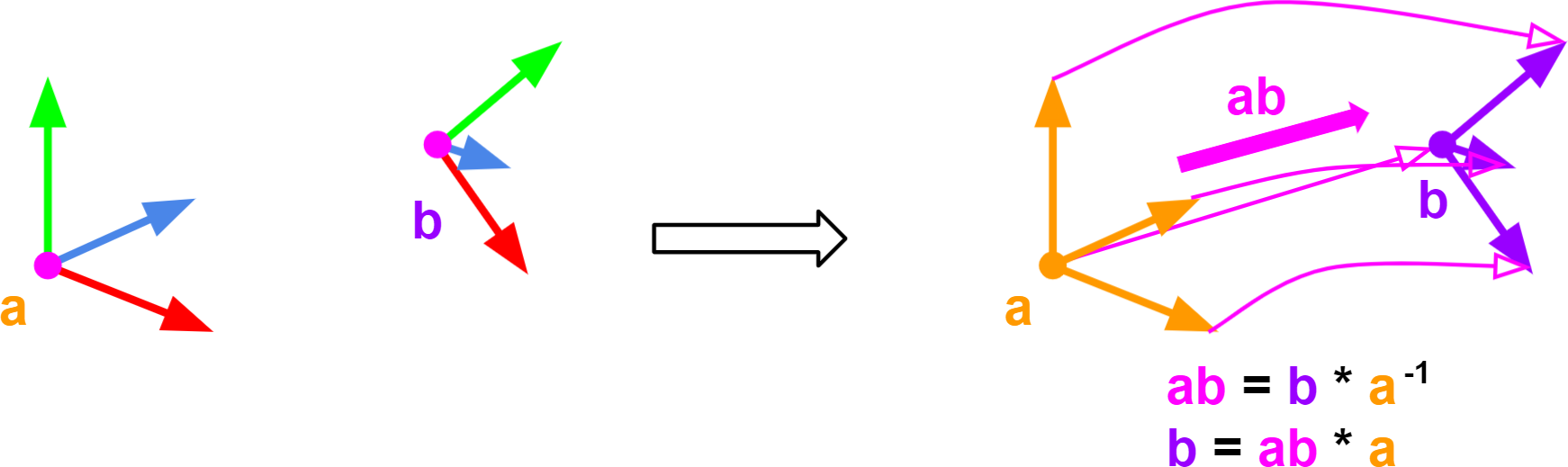
Temos a matriz de transformação ‘a’ e a matriz de transformação ‘b’.
Queremos criar uma matriz ‘ab’ que transforma a matriz ‘a’ na matriz ‘b’.
Lembra que o vetor ‘ab’ (b-a) fez o trabalho na nossa análise de pontos e vetores...
Precisamos fazer algo similar, mas considerando a lógica de combinação de matrizes.
Queremos adicionar ‘b’ e subtrair ‘a’. Para adicionar ‘b’ apenas multiplicamos por ‘b’. Para subtrair ‘a’, multiplicamos pela inversa de ‘a’.
Eu chamei de matriz gradiente ‘ab’ , essa matriz que transforma ‘a’ em ‘b’.
- ‘ab’ = ‘b’*’a’-1
Agora podemos calcular ‘b’ utilizando a equação a seguir:
- ‘b’ = ‘ab’*‘a’
Veja a imagem a seguir:
2.3 Definição da Pose
Uma pose é um conjunto de transformações que definem a forma, silhueta ou relação hierárquica de pai → filho.
Vamos começar definindo uma pose inicial.
Chamaremos essa pose de: bind pose.
Uma forma bastante comum é a chamada T-Pose, como pode ser visto na imagem a seguir:

Agora imagine que queremos modificar nossa bind pose para uma pose alvo: target pose.
O artista pode ajustar as juntas para criar novas poses, como a do exemplo a seguir:

Voltando para a matemática
Considere nossa bind pose como sendo a transformação ‘a’ e a target pose a transformação ‘b’.
Ambas são expressas no espaço de mundo (world space) como a matriz final da transformação.
Veja o exemplo a seguir da bind pose e target pose sobrepostas:
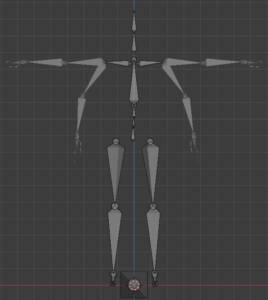
Agora podemos calcular a matriz gradiente ‘ab’ que permite calcular a target pose como uma modificação de nossa bind pose.
- gradient_matrix = ‘ab’ = target_pose * bind_pose-1
- target_pose = gradient_matrix * bind_pose
Na imagem a seguir as setas rosas representam nossas matrizes gradiente:

3 Transformação Ponderada de Vértices
Agora temos uma transformação da bind_pose para a target_pose representadas por uma única matriz.
Podemos fazer algumas manipulações matemáticas misturando nossas matrizes com pontos e vetores (que também são matrizes, mas com 1 coluna e n dimensões).
Isso é o que temos da definição da target_pose:
- gradient_matrix = ‘ab’ = target_pose * bind_pose-1
- target_pose = gradient_matrix * bind_pose << Essa é a parte importante
Imagine que temos um conjunto de vértices no espaço de mundo em relação a nossa T-Pose (bind_pose). Veja a imagem a seguir:

Nós queremos transformar esse conjunto de vértices de acordo com o gradiente que vai da bind_pose para a target_pose.
Podemos expressar a transformação de um vértice como sendo:
- target_point = gradient_matrix * source_point
Essa é a equação principal para expressar a deformação de vértice.
3.1 Interpolação Linear da Matriz Gradiente
Podemos definir a deformação de vértice influenciada por mais de uma junta/matriz.
Essa é a mágica do skinning de mesh.
O artista pode modificar a deformação setando como cada junta/bone afeta cada vértice. No final isso vira uma relação de pesos [0..1].
Podemos pensar da mesma forma que aplicamos transformações, mas ao invés de multiplicar por uma matriz, nós multiplicamos o vértice por várias matrizes, onde cada matriz tem um peso (ou porcentagem de influência na deformação).
A soma desses pesos tem que ser 1.
Isso nos leva a ter uma interpolação linear entre as matrizes das transformações relacionadas. Também chamamos essa relação ponderada de configuração convexa ou relação afim.
Podemos definir a deformação de vértice como:
- target_point = ( gradient_matrix[joint_0] * weight[joint_0] +
gradient_matrix[joint_1] * weight[joint_1] +
... ) * source_point - weight[joint_0] + weight[joint_1] + … = 1
O artista configura as influências no editor 3D através da ferramenta de pintar bones. Esse processo é chamado de rigging. Veja a imagem a seguir:

Com esse gradiente calculado, podemos deformar uma mesh com várias influências.
As ferramentas de pintar influências de juntas/bones geralmente deixam o máximo de 4 influências por vértice. Isso permite que seja otimizado a renderização utilizando skinning na GPU (que falaremos mais tarde).
A imagem abaixo é um exemplo de uma pose definida com os vértices já deformados pela hierarquia:
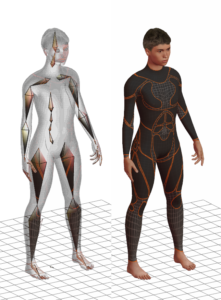
3.2 Prós e Contras
A principal questão de realizar deformação de vértice utilizando uma combinação linear é que isso pode resultar em rotações incorretas, por causa da interpolação linear entre vetores de rotação. O ideal seria realizar uma interpolação diferente para as rotações.
Não é visível na maioria dos casos. Tem trabalhos que estudam outras formas de combinação da matriz de gradiente usando interpolações esféricas ou dual quaternions.
Para aplicações de tempo real, a combinação linear ainda é bastante usada, principalmente porque é rápida e produz bons resultados.
3.3 Algoritmo de Vértice Ponderado
Como calcular as posições de vértices?
Estou considerando que cada vértice já possui um array de influências de juntas/bones.
Pré-Processamento:
* Coordenadas de vértices no espaço de mundo
- Foreach i in vertex.size()
- vertexworld[i] ← localToWorld_matrix * vertex[i]
* Inversa da bind_pose
- Foreach i in bind_pose.size()
- bind_pose_inv[i] ← inverse_matrix( bind_pose[i] )
No Loop Principal:
* Definimos a target_pose como queremos
* Calculamos a matriz gradiente (gradient matrix) para cada junta/bone
- Foreach i in target_pose.size()
- gradient_matrix[i] ← target_pose[i]*bind_pose_inv[i]
* Aplicamos a matriz gradiente para cada vértice
- Foreach i in vertexworld.size()
- gradient ← [0]
- Foreach j in vertex_influence[i].size()
- influence ← vertex_influence[i][j]
- gradient ← gradient + gradient_matrix[influence.bone_index] * influence.weight
- vertexfinal[i] ← gradient * vertexworld[i]
* Finalmente fazemos upload dos dados de vértices para a GPU
3.4 Normais e Tangentes
O que precisamos fazer com as normais e tangentes?
Podemos usar da mesma forma que trabalhamos no vertex shader para consertar a ortogonalidade da normal e tangente.
Ao invés de multiplicar pela matriz gradiente, multiplicamos pela inversa transposta da matriz gradiente.
Pré-Processamento:
* Coordenadas de vértices no espaço de mundo
- Foreach i in vertex.size()
- vertexworld[i] ← localToWorld_matrix * vertex[i]
- N ← transpose(inv(localToWorld_matrix)) * normal[i]
- N ← N / |N| // normalize
- T ← localToWorld_matrix * tangent[i]
- T ← T / |T| // normalize
- T ← T – (T . N)*N // re-orthogonalize the tangent, uses dot product
- T ← T / |T| // normalize
- normalworld[i] ← N
- tangentworld[i] ← T
* Inversa da bind_pose
- Foreach i in bind_pose.size()
- bind_pose_inv[i] ← inverse_matrix( bind_pose[i] )
No Loop Principal:
* Foreach i in vertexworld.size()
- gradient ← [0]
- Foreach j in vertex_influence[i].size()
- influence = vertex_influence[i][j]
- gradient ← gradient + gradient_matrix[influence.bone_index] * influence.weight
- vertexfinal[i] ← gradient * vertexworld[i]
- N ← transpose(inv(gradient)) * normalworld[i]
- N ← N / |N| // normalize
- T ← gradient * tangentworld[i]
- T ← T / |T| // normalize
- T ← T – (T . N)*N // re-orthogonalize the tangent, uses dot product
- T ← T / |T| // normalize
- normalfinal[i] ← N
- tangentfinal[i] ← T
Considerações Finais
O pré-processamento do algoritmo está OK, porque fazemos ele somente uma vez.
O problema está no loop principal porque ele ocorre 60, 75, 120, 240 vezes por segundo.
O cálculo sobre a hierarquia de transformações é próximo de instantâneo, porque contém em torno de 40 nós (juntas/bones) em um personagem humanóide.
Já a multiplicação dos vértices é realizada de 3k até 20k vezes para os vértices, normais e tangentes, de acordo com a complexidade do modelo 3D.
Para Otimizar Mais
Podemos usar a GPU para processar os dados de skinning, transferindo o custo para a GPU.
Assim seria necessário fazer upload de 40 matrizes depois de definir nossa matriz gradiente, ao invés de processar e transmitir de 3k até 20k vértices + normais + tangentes para a GPU todo frame.
4 Skinning na GPU
Podemos usar a GPU para calcular o skinning de vértice. Para isso podemos criar uma estrutura uniform adicional para armazenar nosso array de matrizes gradiente.
Antigamente o limite de matrizes que podiam ser armazenadas no vertex shader era 128, mas atualmente essa quantidade deve ter aumentado.
Além do uniform também precisamos criar 2 novos atributos de vértice: o índice da matriz gradiente usado e o peso dessa matriz. Sendo espertos, podemos usar o tipo vec4 (sequência de 4 floats) para os índices e pesos, o que possibilita a cada vértice ter 4 influências simultâneas.
O que fazemos quando um vértice tiver menos de 4 influências?
Na etapa de pré-processamento podemos calcular todos os índices e pesos normalmente. E quando for preencher os valores dos índices não usados, podemos repetir o acesso à última matriz gradiente e colocar seu peso como 0. Isso fará com que o cache tenha uma vantagem nos valores de matrizes que não afetam os cálculos.
Pré-Processamento
A referência de linguagem de shader que utilizo é o #version 120, para rodar no meu mac de 2011. Ela não permite passar um inteiro como atributo de vértice. Por esse motivo, é necessário criar os valores em float para indexar o array de gradiente.
A estrutura vertex_weight é um array de array que armazena as influências dos vértices. skin_index e skin_weights são array de 4 floats por elementos (vec4).
* skin_index.resize(vertex_weight.size())
* skin_weights.resize(vertex_weight.size())
* Foreach i in vertex_weight.size()
- last_index ← 0
- For j ← 0 to 3
- If j < vertex_weight[i].size()
- last_index ← float(vertex_weight[i][j].bone_index) + 0.2
- skin_index[i][j] ← last_index
- skin_weights[i][j] ← vertex_weight[i][j].weight
- else
- skin_index[i][j] ← last_index
- skin_weights[i][j] ← 0
O novo algoritmo no loop principal
* Definir o target_pose como queremos * Computar a matriz gradiente para cada junta/bone * Fazer upload do array de matriz gradiente para a GPU * Disparar um draw call usando um Vertex Buffer Object estático
No shader, precisamos apenas adicionar o cálculo da matriz final de gradiente antes de usar a posição do vértice como pode ser visto abaixo:
// aSkinIndex and aSkinWeight are 2 new attributes
attribute vec4 aSkinIndex;
attribute vec4 aSkinWeight;
// uSkinGradientMatrix is the gradient matrix array
uniform mat4 uSkinGradientMatrix[32];
mat4 v_gradient_ = mat4(0);
for (int i=0;i<4;i++){
v_gradient_ += uSkinGradientMatrix[int(aSkinIndex[i])] * aSkinWeight[i];
}
vec4 inputPosition = v_gradient_ * aPosition;
…
// normal vertex shader algorithm
...
gl_Position = uMVP * inputPosition;
5 Conclusão
Esse post é o primeiro de três, onde pretendemos abordar o controle de movimentação de personagem 3D.
O próximo será sobre animação esqueletal, não deixe de acompanhar nossas publicações.
Obrigado por ler esse post.
Um abraço,
Alessandro Ribeiro
