Quando você está programando o movimento de um personagem, geralmente é necessário configurar o parâmetro de velocidade.
Em alguns casos, o personagem se move mais rápido, outras vezes ele se move mais devagar, até atingirmos a configuração de parâmetro correta. Este processo pode não funcionar para todas as animações incluídas no projeto.
Neste post abriremos uma discussão sobre como deixar o movimento ser controlado pelo artista. Dessa forma, podemos parar de tentar adivinhar quais são os parâmetros de movimento dos personagens.

1 Contexto
É comum utilizar a movimentação do personagem ou objeto em aplicações interativas (animações ou jogos digitais).
Quando fazemos um controlador de personagem, geralmente colocamos muitos parâmetros para deixá-lo mais flexível e para que possamos aproveitar esse código em vários projetos.
Agora vamos refletir um pouco: Quanto de esforço é necessário para criar um código flexível e adaptável? Em todos os projetos que você já fez, quantas classes de controle de movimentação que você já escreveu?
A principal motivação deste post é levantar mais uma opção para o seu conhecimento tecnológico que pode ser utilizado para criar a movimentação de personagens.
A ideia aqui é deixar que o artista crie a movimentação do personagem no editor 3D que ele já usa.
2 Organização do Esqueleto
Geralmente não existem restrições de como criar um esqueleto para utilizar em um projeto 3D. Mas no nosso caso, precisamos que exista um nó (uma transformação) pai de todas as transformações que chamaremos de nó raiz.
O artista pode criar a animação em todos os nós do esqueleto, mas o movimento ele irá colocar somente no nó raiz.
Com essa restrição, o artista define como a movimentação deve ocorrer e não mais o programador.
O principal benefício do artista definir o deslocamento é que a movimentação do personagem será mais realista.
A imagem abaixo é um exemplo da hierarquia criada pelo MakeHuman para um personagem humanóide:
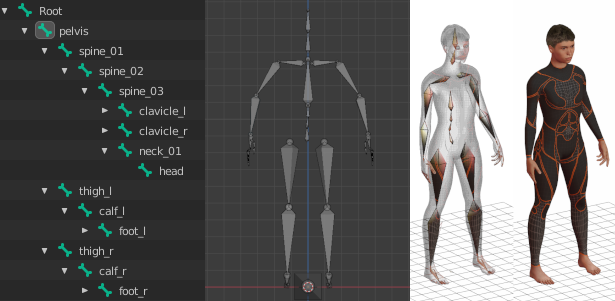
Repare que todos os nós da hierarquia são filhos diretos ou indiretos do nó chamado ‘Root’.
Nesse exemplo, a animação de deslocamento deverá ser atribuída/armazenada no nó Root.
Se você quiser ver mais detalhes de como armazenar e processar as animações, pode ver nosso post sobre animação esqueletal.
3 Algoritmo
Agora que já temos uma animação no nó raiz, podemos partir para a implementação.
Quando estamos trabalhando com uma animação, ela pode ser cíclica ou ser reproduzida uma única vez.
O caso mais complexo é a animação cíclica, pois se deve definir o que acontece quando a animação é reiniciada. Ao contrário dos outros posts, abordaremos o caso mais complexo. É bastante comum ter este tipo de animação (exemplo: walk cycle).
Observação: Quando usamos a informação do nó raiz para movimentar o personagem 3D, nós não iremos aplicar a transformação ao personagem (exemplo: skinning). Ao invés disso, iremos descobrir qual o delta, ou variação, que devemos aplicar ao nó raiz que contém o modelo 3D do nosso personagem.
3.1 Sequência Não Cíclica
Esse é o caso mais simples, apenas precisamos calcular qual a posição final que o nó terá de acordo com a animação, e utilizar essa informação para modificar a posição do personagem no mundo.
No método de atualização (update) devemos aplicar a animação no nó raiz, armazenar essa posição, setar a posição do nó raiz para a posição inicial e calcular qual a variação que deve ser aplicada no nó do personagem.
Veja a imagem abaixo:
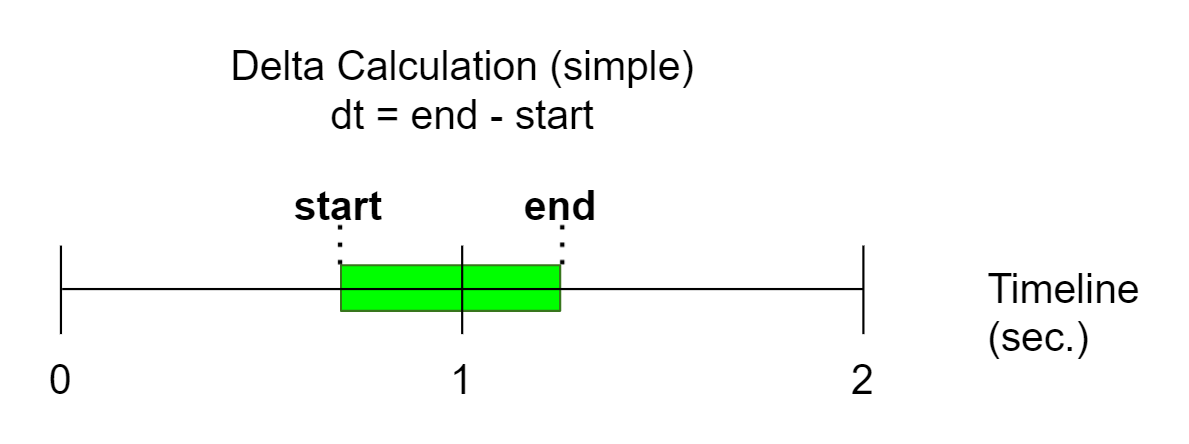
Como a variação de tempo apenas aumenta, o cálculo do delta também é direto.
O algoritmo fica da seguinte forma:
- Update
- previous_position_world ← root.getLocalToWorldMatrix() * [0,0,0]T
- Transform the root node as its animation channel wants
- new_position_world ← root.getLocalToWorldMatrix() * [0,0,0]T
- root.setPositionFromWorldSpace( previous_position_world )
- delta_world ← new_position_world - previous_position_world
- characterNode.translate(delta_world)
3.2 Sequência Cíclica
Podem existir duas situações negativas quando tratamos a animação cíclica:
- O algoritmo pode considerar um delta de movimento muito grande quando o tempo da animação passa por 0 (e o mesmo é reiniciado).
- Quando a animação é curta, e o tempo elapsed é maior. O caso ideal é que considere as várias vezes que a animação deverá rodar para realizar o deslocamento correto. Se não considerar isso, o personagem poderá se movimentar pouco em relação ao que deveria ser movimentado.
A solução para a primeira situação é utilizar um cálculo do delta que ocorre entre os frames da animação. No segundo caso, deixo aberto para você pensar na solução.
Vamos usar o algoritmo do nosso post anterior e incrementá-lo para detectar quando o tempo passa pelo quadro-chave 0. Dessa forma, podemos adicionar uma contagem do delta no final da animação mais o delta no início da animação.
Veja a imagem abaixo:
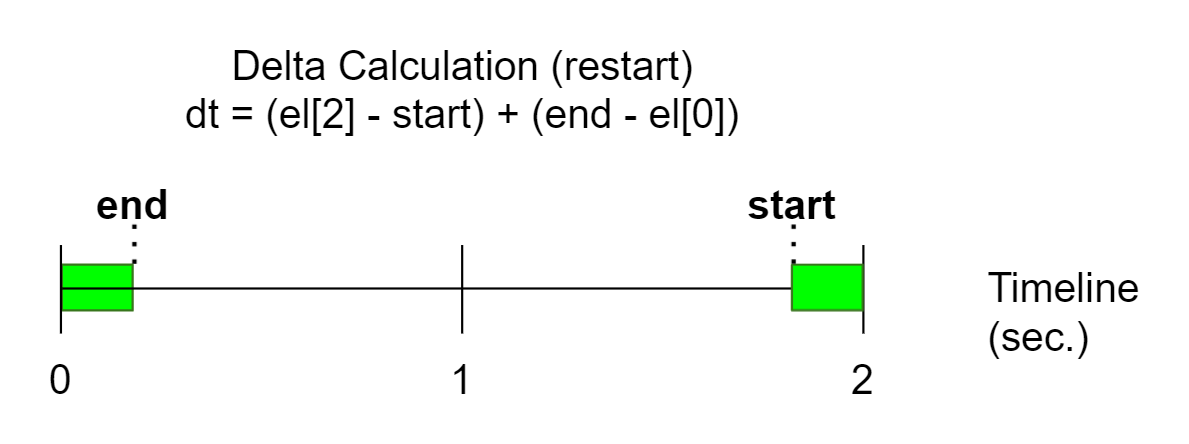
Nesta situação, ao realizar o incremento de tempo, ele pode ser reiniciado considerando o tempo total da linha do tempo.
Quando essa situação ocorre, precisamos calcular o delta do início do incremento ao final da linha do tempo somado com o início da linha do tempo com o final do incremento.
Veja o algoritmo abaixo:
class QueryInterpolationPos {
public:
void QueryInterpolationPos() {
lastIndexA = -1;
lastIndexB = -1;
lastLrp = 0.0f;
lastTimeQuery = 0.0f;
}
void queryInterval_ForwardLoop(
const std::vector<KeyframePos> &channel, float time,
KeyframePos **out_A, KeyframePos **out_B, float *out_lrp,
vec3 *interquery_delta = NULL ) {
if (lastIndexA == -1) {
// initialize data
lastIndexA = 0;
lastIndexB = 1;
lastLrp = 0.0f;
lastTimeQuery = channel[0].time;
}
if (channel.size() == 0) {
*out_A = *out_B = NULL;
*out_lrp = 0.0f;
// new code
if (interquery_delta != NULL)
*interquery_delta = vec3(0);
return;
} else if (channel.size() == 1) {
*out_A = *out_B = &channel[0];
*out_lrp = 0.0f;
// new code
if (interquery_delta != NULL)
*interquery_delta = vec3(0);
return;
}
time = clamp(time, channel[0].time, channel[channel.size() - 1].time);
if (time < lastTimeQuery) {
// new code
if (interquery_delta != NULL) {
vec3 lastReturned = lerp(channel[lastIndexA].pos, channel[lastIndexB].pos, lastLrp);
*interquery_delta = channel[channel.size() - 1].pos - lastReturned;
}
// reset query
lastIndexA = 0;
lastIndexB = 1;
lastLrp = 0.0f;
lastTimeQuery = channel[0].time;
} else {
// new code
if (interquery_delta != NULL)
*interquery_delta = vec3(0);
}
vec3 lastReturned;
if (time > lastTimeQuery) {
// new code
if (interquery_delta != NULL)
lastReturned = lerp(channel[lastIndexA].pos, channel[lastIndexB].pos, lastLrp);
lastTimeQuery = time;
for (; lastIndexA < channel.size() - 2; lastIndexA++) {
if (time < channel[lastIndexA + 1].time)
break;
}
lastIndexB = lastIndexA + 1;
} else {
// same time query
*out_A = &channel[lastIndexA];
*out_B = &channel[lastIndexB];
*out_lrp = lastLrp;
return;
}
float delta = (channel[lastIndexB].time - channel[lastIndexA].time);
if (delta <= 1.0e-6)
lastLrp = 0.0f;
else
lastLrp = (time - channel[lastIndexA].time) / delta;
// new code
if (interquery_delta != NULL) {
vec3 result = lerp(channel[lastIndexA].pos, channel[lastIndexB].pos, lastLrp);
*interquery_delta += result - lastReturned;
}
*out_A = &channel[lastIndexA];
*out_B = &channel[lastIndexB];
*out_lrp = lastLrp;
}
};
Note que utilizamos o comentário '// new code' nas partes do algoritmo que foram modificadas.
Nosso método de interpolação agora retorna a variação que ocorreu de um frame para o outro através do parâmetro de retorno 'interquery_delta'.
Agora podemos criar um algoritmo de controle do nosso personagem.
Veja o algoritmo abaixo:
class TransformAnimation {
public:
std::vector<KeyframePos> channelPosition;
QueryInterpolationPos queryInterpolationPos;
std::vector<KeyframeRot> channelRotation;
QueryInterpolationRot queryInterpolationRot;
// root motion variables
bool process_as_root;
vec3 start_position_local;
TransformAnimation() {
this->process_as_root = false;
}
// should call this after fill at least
// the first frame of the position channel
void initialize(bool process_as_root) {
this->process_as_root = process_as_root;
if (process_as_root)
start_position_local = channelPosition[0].value;
}
vec3 queryPosition(float time, vec3 *interquery_delta_local = NULL) {
KeyframePos *out_A, *out_B;
float out_lrp;
if (!process_as_root)
interquery_delta_local = NULL;
queryInterpolationPos.queryInterval_ForwardLoop(
&channelPosition, time, // vector, seconds
&out_A, &out_B, &out_lrp, // output parameters
interquery_delta_local
);
if (out_A == NULL)
return vec3(0);
if (process_as_root) {
return start_position_local;
} else
return lerp( out_A->pos, out_B->pos, out_lrp);
}
quat queryRotation(float time) {
KeyframeRot *out_A, *out_B;
float out_lrp;
queryInterpolationRot.queryInterval_ForwardLoop(
&channelRotation, time, // vector, seconds
&out_A, &out_B, &out_lrp // output parameters
);
if (out_A == NULL)
return quat(0,0,0,1);
return slerp( out_A->rot, out_B->rot, out_lrp);
}
mat4 computeMatrix(float time, vec3 *interquery_delta = NULL) {
vec3 pos = queryPosition(time, interquery_delta);
quat rot = queryRotation(time);
return translateMatrix(pos) * quat2Mat4(rot);
}
};
Note que devemos chamar o método 'initialize' e indicar se esse nó de animação é o root ou não.
No caso de ser o root, nós podemos utilizar o parâmetro de retorno 'interquery_delta' para deslocar nosso personagem.
Agora utilizando essa classe podemos animar nosso personagem da seguinte forma:
float anim_duration = ...;
TransformAnimation root_anim;
// ... fill the animation channels
root_anim.initialize(true);
// auxiliary variables
vec3 interquery_delta;
vec3 world_pos = vec3(0,0,0);
float anim_time = 0.0f;
// now the update
void Update(float elapsed_sec) {
anim_time = fmod(anim_time + elapsed_sec, anim_duration);
mat4 render_matrix = root_anim.computeMatrix(anim_time, &interquery_delta);
// finally move the character
world_pos = world_pos + interquery_delta;
mat4 character_move_transform = translateMatrix(world_pos) * render_matrix;
// ...
}
4 Conclusão
Com esse post fechamos os conceitos básicos para tratar a movimentação de personagens.
Quando eu estava escrevendo todos esses posts, acabei notando que poderia acrescentar algumas características de movimentação ligadas à Unity3D. Assim criei o asset: http://u3d.as/2F6K
Eu agradeço caso você possa me ajudar comprando esse asset.
Tenho também uma implementação de referência no meu framework em OpenGL que pode ser visto no projeto tech-demo-animation. Esse demo aborda: skinning de mesh, animação esqueletal e movimentação pelo nó root. Tudo em um só projeto.
Eu fiz esse vídeo no Youtube para explicar todo o conteúdo relativo à movimentação de personagem. Ele aborda skinning de mesh, animação esqueletal e movimentação pelo nó root.
Obrigado por ler esse post.
Um abraço,
Alessandro Ribeiro
