Um certo tempo atrás eu vi uma dúvida de uma pessoa iniciante no mundo de CG a respeito do que seria a interpolação nos shaders.
Acho que esse tópico pode ser interessante para quem está se familiarizando com o tema.
Aqui falarei do conceito básico que está por trás da interpolação que é realizada dentro dos shaders.
Relação Linear
No espaço afim (da geometria) existe uma relação especial chamada de configuração convexa, relação linear, etc…
Existem vários nomes para a mesma coisa. Aqui vamos adotar o nome relação linear.
Imagine que podemos definir um ponto ‘P’ que é o resultado da soma de outros pontos ‘A’+ ‘B’+ ‘C’+ ‘D’+ ‘E’+ …
P = A + B + C + D + E + ...
Agora vamos reescrever essa equação adicionando pesos que são multiplicados para cada ponto de entrada:
P = kA + lB + mC + nD + oE + ...
Cada peso pode ser qualquer número.
Tem uma situação especial em relação a esses pesos: Quando a soma de todos é igual a ‘1’, então temos uma relação linear.
k+l+m+n+o+... = 1
O Caso do Triângulo
Para formar um triângulo precisamos de 3 pontos.
A relação linear quando temos 3 pontos de entrada é chamada de coordenadas baricêntricas.
E essa é a equação da relação linear para um triângulo:
P = kA + lB + mC, k+l+m=1
Com essa equação, podemos definir qualquer ponto ‘P’ que é o resultado da soma ponderada dos 3 pontos do triângulo.
Nos Shaders
A relação linear é utilizada nos shaders por debaixo dos panos.
Todas as variáveis que são passadas do vertex shader para o fragment shader passam pelo processo de interpolação.
A) A Saída do Vertex Shader gera a Base para a Rasterização
Sempre que o contador de primitivas chega até 3, a placa de vídeo dispara a rasterização desse triângulo.
O resultado da rasterização são todos os fragmentos dentro do triângulo que podem ou não virar um pixel no final.
Todos os fragmentos que irão virar um pixel são enviados para o fragment shader.
É ai que a coisa fica interessante.
B) Os Fragmentos que Irão Virar Pixels
Esses fragmentos possuem uma posição no espaço projetivo.
Internamente as placas de vídeo calculam os pesos da relação linear relativa a esse fragmento que foi gerado.
Olhe a equação novamente:
P = kA + lB + mC, k+l+m=1
Aqui ‘P’ é a posição do fragmento, e ‘A’, ‘B’, ‘C’ a posição dos pontos do triângulo depois da projeção.
Para cada fragmento podemos calcular os pesos ‘k, l, m’ dessa equação.
Podemos usar a equação da coordenada baricêntrica para calcular esses coeficientes.
Coordenada Baricêntrica
A coordenada baricêntrica do triângulo pode ser calculada usando a relação de áreas dos triângulos internos que são formados.
Veja a imagem abaixo:
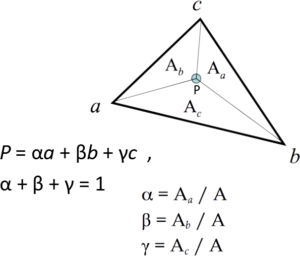
Assim podemos calcular os pesos ‘k, l, m’ dividindo a área de cada triângulo menor pela área do triângulo maior.
Podemos utilizar o produto vetorial das arestas para calcular as áreas dos triângulos.
O módulo do produto vetorial é a área do quadrilátero formado pelas arestas.
Para calcular a área dos triângulo, basta dividir por 2.
Veja o exemplo de um algoritmo:
vec3 baricentricCoord(vec3 a, vec3 b, vec3 c, vec3 p){
vec3 bc = c-b;
vec3 ba = a-b;
vec3 cross_bc_ba = cross(bc,ba);
vec3 N = normalize(cross_bc_ba);
float areaTriangle_times_2 = dot(cross_bc_ba,N);
float areaTriangle_inv_div_2 = 1.0 / areaTriangle_times_2;
vec3 bp = p-b;
vec3 uvw;
uvw.x = dot(cross(bc,bp),N); // internal triangle area * 2
uvw.z = dot(cross(bp,ba),N); // internal triangle area * 2
uvw.xz = uvw.xz * areaTriangle_inv_div_2; // simplification: 2 / 2
uvw.y = 1.0 - uvw.x - uvw.z;
return uvw;
}
É importante lembrar que temos que calcular a área dos triângulos com o sinal, para que a relação linear seja mantida.
C) Os Pesos ‘k, l, m’ Já Estão Calculados para Cada Fragmento
De posse dos pesos ‘k, l, m’ podemos aplicar a relação linear para qualquer outra variável.
Apenas precisamos manter esses pesos e substituir o que está sendo interpolado.
Exemplo:
Imagine que temos uma cor para cada ponto do triângulo: C1, C2 e C3.
Eu vou usar esses coeficientes para criar uma nova relação linear:
Cf = kC1 + lC2 + mC3, k+l+m=1
‘Cf’ é a cor do fragmento, que é o resultado da interpolação das três cores C1, C2 e C3 relacionadas ao triângulo.
Outro Exemplo:
Imagine que temos uma coordenada UV para cada ponto do triângulo: UV1, UV2 e UV3.
UVf = kUV1 + lUV2 + mUV3, k+l+m=1
‘UVf’ é a coordenada uv do fragmento, que é o resultado da interpolação das três coordenadas uv: UV1, UV2 e UV3 relacionadas ao triângulo.
D) GLSL – Como Implementar?
Como eu disse anteriormente, todas as variáveis que são passadas do vertex shader para o fragment shader passam por esse processo de interpolação.
#version 120
Nessa versão do GLSL, usamos o nome especial ‘varying’.
Veja o exemplo do vertex shader:
#version 120
attribute vec4 aPosition;
attribute vec2 aUV0;
uniform mat4 uMVP; // ModelViewProjection matrix
varying vec2 Frag_UV;
void main(){
Frag_UV = aUV0;
gl_Position = uMVP * aPosition;
}
Veja o exemplo do fragment shader:
#version 120
uniform sampler2D uTextureAlbedo;
varying vec2 Frag_UV;
void main(){
vec4 texel = texture2D(uTextureAlbedo, Frag_UV);
gl_FragColor = texel;
}
Aqui ‘Frag_UV’ passou pelo processo de interpolação.
#version 130 e Superior
Nessas versões do GLSL, usamos os nomes especiais: ‘out’ no vertex shader e ‘in’ no fragment shader.
Veja o exemplo do vertex shader:
#version 150
in vec4 aPosition;
in vec2 aUV0;
uniform mat4 uMVP; // ModelViewProjection matrix
out vec2 Frag_UV;
void main(){
Frag_UV = aUV0;
gl_Position = uMVP * aPosition;
}
Veja o exemplo do fragment shader:
#version 150
uniform sampler2D uTextureAlbedo;
in vec2 Frag_UV;
out vec4 Out_Color;
void main(){
vec4 texel = texture2D(uTextureAlbedo, Frag_UV);
Out_Color = texel;
}
Aqui ‘Frag_UV’ passou pelo processo de interpolação.
Conclusão
E essa é a mágica que ocorre quando passamos um valor do vertex shader para o fragment shader.
Espero que tenham gostado.
Abraços!
Alessandro Ribeiro.
