No nosso post anterior, falamos do radix sort em combinação com o counting sort, que é mais rápido que o algoritmo padrão std::sort.
Olhando para o algoritmo original, é possível fazer mais algumas otimizações.
Nossa saga em busca da ordenação mais rápida continua.
Relembrando Nosso Algoritmo
Para cada um dos 4 bytes do inteiro deve ser realizada a sequência:
- Zerar array de contagem
- Contar o byte atual
- Calcular os offsets
- Posicionar os elementos nas posições ordenadas desse byte
- Fazer swap do array de entrara/saida
Veja o algoritmo abaixo:
for (i = 0; i < 4; i++){
// clear counting array
memset(counting, 0, sizeof(uint32) * 256);
// count current byte
for (j = 0; j < N; j++){
index = (in[j] >> (i<<3) ) & 0xff;
counting[index]++;
}
// compute offset
acc = counting[0];
counting[0] = 0;
for (j = 1; j < 256; j++){
tmp1 = counting[j];
counting[j] = acc;
acc += tmp1;
}
// place elements in the output array
for (j = 0; j < N; j++){
index = (in[j] >> (i<<3) ) & 0xff;
out_index = counting[index];
counting[index]++;
out[out_index] = in[j];
}
//swap out, in
tmp = in;
in = out;
out = tmp;
}
Como Otimizar?
Nós já sabemos que a demanda de computação desse algoritmo é baixa, mas em contrapartida, a demanda de movimentação de dados dele é alta.
1ª Estratégia: Evitar de percorrer o array de entrada várias vezes
A primeira estratégia de otimização é tentar evitar percorrer o array de entrada o máximo possível.
No início do algoritmo nós percorremos o array de entrada 4 vezes, e montamos 4 vezes o array de contagem de elementos.
Podemos tirar a computação do array de contagem para fora do loop maior, e percorrer o array de entrada apenas uma vez e montar 4 arrays de contagem simultaneamente.
O principal fator negativo dessa abordagem é que agora, será necessário alocar um array de contagem pra cada byte, ou seja, precisaremos de 4 vezes o tamanho do array atual.
Isso deve dar em torno de 4KBytes para nosso array de contagem.
Para isso, será necessário criar um array de contagem 4 vezes maior.
Veja o código abaixo:
// clear counting array
memset(&counting[0][0], 0, sizeof(uint32) * 256 * 4);
// count current byte
for (j = 0; j < N; j++){
counting[(in[j] >> 0 ) & 0xff][0]++;
counting[(in[j] >> 8 ) & 0xff][1]++;
counting[(in[j] >> 16 ) & 0xff][2]++;
counting[(in[j] >> 24 ) & 0xff][3]++;
}
// compute offset
uint32_t acc[4] = {
counting[0][0],
counting[0][1],
counting[0][2],
counting[0][3]
};
counting[0][0] = 0;
counting[0][1] = 0;
counting[0][2] = 0;
counting[0][3] = 0;
for (j = 1; j < 256; j++){
uint32_t tmp[4] = {
counting[j][0],
counting[j][1],
counting[j][2],
counting[j][3]
};
counting[j][0] = acc[0];
counting[j][1] = acc[1];
counting[j][2] = acc[2];
counting[j][3] = acc[3];
acc[0] += tmp[0];
acc[1] += tmp[1];
acc[2] += tmp[2];
acc[3] += tmp[3];
}
// O restante do algoritmo continua igual
for (i = 0; i < 4; i++){
// place elements in the output array
for (j = 0; j < N; j++){
index = (in[j] >> (i<<3) ) & 0xff;
out_index = counting[index][i];
counting[index][i]++;
out[out_index] = in[j];
}
//swap out, in
tmp = in;
in = out;
out = tmp;
}
2ª Estratégia: Usar Instruções SSE2 para realizar 4 operações inteiras com uma instrução
A segunda estratégia é utilizar as instruções SSE2 para realizar 4 operações com inteiros usando uma única instrução.
Aqui o ganho será pouco, mas é importante, uma vez que é aplicado no cálculo de offset do array de contagem.
3ª Estratégia: Fazer unroll do loop maior de 4 iterações
E a terceira estratégia é fazer um loop unroll no for maior (o que repete 4 vezes).
Pode parecer uma estratégia desnecessária, mas esse unroll permite substituir várias variáveis por constantes da iteração final.
Algoritmo Final
// 1ª otimização: calcular o array counting fora do loop principal
// 2ª otimização: usar SSE2
// 3ª otimização: loop unroll
#if _MSC_VER
#define _mm_i32_(v,i) (v).m128i_i32[i]
#else
#define _mm_i32_(v,i) ((int32_t*)&(v))[i]
#endif
__m128i counting[256];
memset(counting, 0, sizeof(__m128i) * 256);
// count all bytes
for (j = 0; j < N; j++){
_mm_i32_(counting[(in[j]) & 0xff], 0)++;
_mm_i32_(counting[(in[j] >> 8) & 0xff], 1)++;
_mm_i32_(counting[(in[j] >> 16) & 0xff], 2)++;
_mm_i32_(counting[(in[j] >> 24) & 0xff], 3)++;
}
//compute offsets
__m128i acc = counting[0];
counting[0] = _mm_set1_epi32(0);
for (uint32_t j = 1; j < 256; j++) {
__m128i tmp = counting[j];
counting[j] = acc;
acc = _mm_add_epi32(acc, tmp);
}
const __m128i _c_0 = _mm_setr_epi32(1, 0, 0, 0);
const __m128i _c_1 = _mm_setr_epi32(0, 1, 0, 0);
const __m128i _c_2 = _mm_setr_epi32(0, 0, 1, 0);
const __m128i _c_3 = _mm_setr_epi32(0, 0, 0, 1);
//shift = 0
{
// place elements in the output array
for (uint32_t j = 0; j < arrSize; j++) {
uint32_t currItem = in[j];
uint32_t bucket_index = ((currItem) & 0xff);
uint32_t out_index = _mm_i32_(counting[bucket_index], 0);
counting[bucket_index] = _mm_add_epi32(counting[bucket_index], _c_0);
out[out_index] = currItem;
}
//swap out, in
uint32_t* tmp = in;
in = out;
out = tmp;
}
//shift = 8
{
// place elements in the output array
for (uint32_t j = 0; j < arrSize; j++) {
uint32_t currItem = in[j];
uint32_t bucket_index = ((currItem >> 8) & 0xff);
uint32_t out_index = _mm_i32_(counting[bucket_index], 1);
counting[bucket_index] = _mm_add_epi32(counting[bucket_index], _c_1);
out[out_index] = currItem;
}
//swap out, in
uint32_t* tmp = in;
in = out;
out = tmp;
}
//shift = 16
{
// place elements in the output array
for (uint32_t j = 0; j < arrSize; j++) {
uint32_t currItem = in[j];
uint32_t bucket_index = ((currItem >> 16) & 0xff);
uint32_t out_index = _mm_i32_(counting[bucket_index], 2);
counting[bucket_index] = _mm_add_epi32(counting[bucket_index], _c_2);
out[out_index] = currItem;
}
//swap out, in
uint32_t* tmp = in;
in = out;
out = tmp;
}
//shift = 24
{
// place elements in the output array
for (uint32_t j = 0; j < arrSize; j++) {
uint32_t currItem = in[j];
uint32_t bucket_index = ((currItem >> 24) & 0xff);
uint32_t out_index = _mm_i32_(counting[bucket_index], 3);
counting[bucket_index] = _mm_add_epi32(counting[bucket_index], _c_3);
out[out_index] = currItem;
}
//swap out, in
uint32_t* tmp = in;
in = out;
out = tmp;
}
O código fonte está disponível: aqui.
Resultado
A tabela abaixo mostra os tempos do nosso algoritmo base comparado com a versão otimizada usando SSE.
Execution Time Radixsort vs Radixsort SSE (secs)
| amount (Mega) | radixsort | radixsort SSE |
|---|---|---|
| 0,1 | 0,000999 | 0,000569 |
| 0,5 | 0,004812 | 0,002236 |
| 1 | 0,009914 | 0,004855 |
| 5 | 0,050997 | 0,024821 |
| 10 | 0,101511 | 0,050143 |
| 50 | 0,510289 | 0,255025 |
| 100 | 1,025262 | 0,499212 |
| 500 | 5,125806 | 2,598452 |
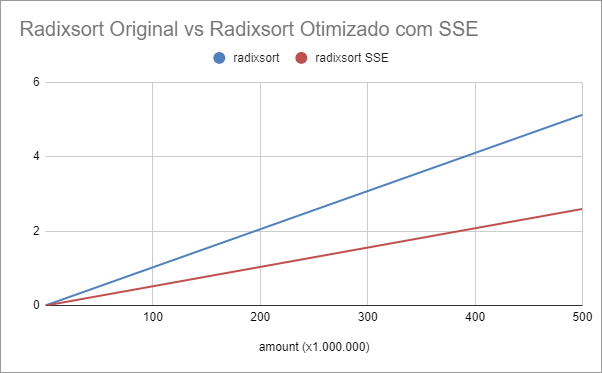
O algoritmo modificado com o SSE, tem um speedup médio de 2.
Veja o gráfico comparativo do tempo de resposta em segundos abaixo:
Conclusão
Das três estratégias apresentadas anteriormente, a que tem mais impacto, devido à natureza do algoritmo é a eliminação de percorrimentos no array de entrada.
Utilizar SSE e o loop unroll tem um impacto menor no desempenho geral do algoritmo.
Um fato interessante é que a versão paralela agora apresenta um ganho muito baixo comparado com a versão otimizada do algoritmo.
O que reforça o pensamento de que o tempo de execução desse algoritmo sofre mais influência das movimentações na memória do que computações na CPU.
Espero que tenham gostado do conteúdo.
abraços,
Alessandro Ribeiro
