A while ago I saw a question from a beginner in the world of CG about what would be the interpolation in shaders.
I think this topic can be interesting for those who are getting familiar with the topic.
Here I will talk about the basic concept behind the interpolation that is performed inside shaders.
Linear Relationship
In affine space (of geometry) there is a special relationship called convex configuration, linear relationship, etc…
There are several names for the same thing. Here we will adopt the name linear relation.
Imagine that we can define a point 'P' which is the result of the sum of other points: ‘A’+ ‘B’+ ‘C’+ ‘D’+ ‘E’+ ….
P = A + B + C + D + E + ...
Now let's rewrite this equation by adding weights that are multiplied for each input point:
P = kA + lB + mC + nD + oE + ...
Each weight can be any number.
There is a special situation regarding these weights: When the sum of all is equal to '1', then we have a linear relationship.
k+l+m+n+o+... = 1
The Triangle Case
To form a triangle we need 3 points.
The linear relationship when we have 3 entry points is called barycentric coordinates.
And this is the equation of the linear relationship for a triangle:
P = kA + lB + mC, k+l+m=1
With this equation, we can define any point 'P' which is the result of the weighted sum of the 3 points of the triangle.
The Shaders
The linear relationship is used in shaders under the hood.
All variables that are passed from the vertex shader to the fragment shader go through the interpolation process.
A) The Vertex Shader Output generates the Basis for the Rasterization
Whenever the primitives counter reaches 3, the video card triggers the rasterization of this triangle.
The result of the rasterization is all the fragments inside the triangle that may or may not become a pixel at the end.
All the fragments that will become a pixel are sent to the fragment shader.
That's where things get interesting.
B) The Fragments That Will Become Pixels
These fragments have a position in projective space.
Internally, the video cards calculate the weights of the linear relation relative to that fragment that was generated.
Look at the equation again:
P = kA + lB + mC, k+l+m=1
Here 'P' is the position of the fragment, and 'A', 'B', 'C' the position of the triangle points after the projection.
For each fragment we can calculate the 'k, l, m' weights of this equation.
We can use the barycentric coordinate equation to calculate these coefficients.
Barycentric Coordinate
The barycentric coordinate of the triangle can be calculated using the ratio of areas of the inner triangles that are formed.
See the image below:
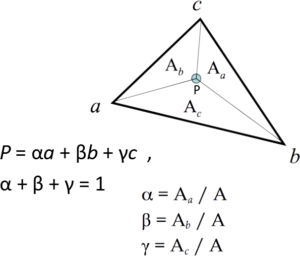
So we can calculate the weights 'k, l, m' dividing the area of each smaller triangle by the area of the larger triangle.
We can use the cross product of edges to calculate the areas of triangles.
The magnitude of the cross product is the area of the quadrilateral formed by the edges.
To calculate the area of triangles, simply divide by 2.
Here's an example of an algorithm:
vec3 baricentricCoord(vec3 a, vec3 b, vec3 c, vec3 p){
vec3 bc = c-b;
vec3 ba = a-b;
vec3 cross_bc_ba = cross(bc,ba);
vec3 N = normalize(cross_bc_ba);
float areaTriangle_times_2 = dot(cross_bc_ba,N);
float areaTriangle_inv_div_2 = 1.0 / areaTriangle_times_2;
vec3 bp = p-b;
vec3 uvw;
uvw.x = dot(cross(bc,bp),N); // internal triangle area * 2
uvw.z = dot(cross(bp,ba),N); // internal triangle area * 2
uvw.xz = uvw.xz * areaTriangle_inv_div_2; // simplification: 2 / 2
uvw.y = 1.0 - uvw.x - uvw.z;
return uvw;
}
It is important to remember that we have to calculate the area of the triangles with the sign, so that the linear relationship is maintained.
C) Weights 'k, l, m' are Already Calculated for Each Fragment
With the weights 'k, l, m' we can apply the linear relationship to any other variable.
We just need to keep these weights and replace what is being interpolated.
Example:
Imagine that we have a color for each point of the triangle: C1, C2 and C3.
I'm going to use these coefficients to create a new linear relationship:
Cf = kC1 + lC2 + mC3, k+l+m=1
‘Cf’ is the color of the fragment, which is the result of interpolation of the three colors C1, C2 and C3 related to the triangle.
Another Example:
Imagine that we have a UV coordinate for each point of the triangle: UV1, UV2 and UV3.
UVf = kUV1 + lUV2 + mUV3, k+l+m=1
‘UVf’ is the uv coordinate of the fragment, which is the result of interpolation of the three uv coordinates: UV1, UV2 and UV3 related to the triangle.
D) GLSL – How to Implement?
As I said earlier, all variables that are passed from the vertex shader to the fragment shader go through this interpolation process.
#version 120
In this version of GLSL, we use the special name 'varying'.
See the example of the vertex shader:
#version 120
attribute vec4 aPosition;
attribute vec2 aUV0;
uniform mat4 uMVP; // ModelViewProjection matrix
varying vec2 Frag_UV;
void main(){
Frag_UV = aUV0;
gl_Position = uMVP * aPosition;
}
See the example of the fragment shader:
#version 120
uniform sampler2D uTextureAlbedo;
varying vec2 Frag_UV;
void main(){
vec4 texel = texture2D(uTextureAlbedo, Frag_UV);
gl_FragColor = texel;
}
Here 'Frag_UV' passed through the interpolation process.
#version 130 and Above
In these versions of GLSL, we use special names: 'out' in the vertex shader and 'in' in the fragment shader.
See the example of the vertex shader:
#version 150
in vec4 aPosition;
in vec2 aUV0;
uniform mat4 uMVP; // ModelViewProjection matrix
out vec2 Frag_UV;
void main(){
Frag_UV = aUV0;
gl_Position = uMVP * aPosition;
}
See the example of the fragment shader:
#version 150
uniform sampler2D uTextureAlbedo;
in vec2 Frag_UV;
out vec4 Out_Color;
void main(){
vec4 texel = texture2D(uTextureAlbedo, Frag_UV);
Out_Color = texel;
}
Here 'Frag_UV' passed through the interpolation process.
Conclusion
And this is the magic that happens when we pass a value from the vertex shader to the fragment shader.
I hope you like it.
Best regards.
Alessandro Ribeiro.
