In our previous post, we talked about radix sort in combination with count sort, which is faster than the standard std::sort algorithm.
Looking at the original algorithm, it is possible to optimize it more.
Our quest for faster sorting continues.
Remembering Our Algorithm
For each of the 4 bytes of the integer, the following sequence must be done:
- Fill with zeros the count array
- Count the current byte
- Compute the offsets
- Position the elements in their positions for this byte
- Swap the in/out array
See the algorithm below:
for (i = 0; i < 4; i++){
// clear counting array
memset(counting, 0, sizeof(uint32) * 256);
// count current byte
for (j = 0; j < N; j++){
index = (in[j] >> (i<<3) ) & 0xff;
counting[index]++;
}
// compute offset
acc = counting[0];
counting[0] = 0;
for (j = 1; j < 256; j++){
tmp1 = counting[j];
counting[j] = acc;
acc += tmp1;
}
// place elements in the output array
for (j = 0; j < N; j++){
index = (in[j] >> (i<<3) ) & 0xff;
out_index = counting[index];
counting[index]++;
out[out_index] = in[j];
}
//swap out, in
tmp = in;
in = out;
out = tmp;
}
How to Optimize?
We already know that the computing demand of this algorithm is low, but on the other hand, the data movement demand of it is high.
1st Strategy: Avoid iterate over the input array several times
The first optimization strategy is to try to avoid traversing the input array as much as possible.
At the beginning of the algorithm we loop through the input array 4 times, and compute the element count array 4 times.
We can take the count array computation out of the larger loop, and loop through the input array just once and build 4 count arrays simultaneously.
The main negative factor of this approach is that now, it will be necessary to allocate a counting array for each byte, that is, we will need 4 times the size of the current array.
That should be around 4KBytes for our count array.
For this, it will be necessary to create a count array 4 times larger.
See the code below:
// clear counting array
memset(&counting[0][0], 0, sizeof(uint32) * 256 * 4);
// count current byte
for (j = 0; j < N; j++){
counting[(in[j] >> 0 ) & 0xff][0]++;
counting[(in[j] >> 8 ) & 0xff][1]++;
counting[(in[j] >> 16 ) & 0xff][2]++;
counting[(in[j] >> 24 ) & 0xff][3]++;
}
// compute offset
uint32_t acc[4] = {
counting[0][0],
counting[0][1],
counting[0][2],
counting[0][3]
};
counting[0][0] = 0;
counting[0][1] = 0;
counting[0][2] = 0;
counting[0][3] = 0;
for (j = 1; j < 256; j++){
uint32_t tmp[4] = {
counting[j][0],
counting[j][1],
counting[j][2],
counting[j][3]
};
counting[j][0] = acc[0];
counting[j][1] = acc[1];
counting[j][2] = acc[2];
counting[j][3] = acc[3];
acc[0] += tmp[0];
acc[1] += tmp[1];
acc[2] += tmp[2];
acc[3] += tmp[3];
}
// The rest of the algorithm remains the same.
for (i = 0; i < 4; i++){
// place elements in the output array
for (j = 0; j < N; j++){
index = (in[j] >> (i<<3) ) & 0xff;
out_index = counting[index][i];
counting[index][i]++;
out[out_index] = in[j];
}
//swap out, in
tmp = in;
in = out;
out = tmp;
}
2nd Strategy: Use SSE2 Instructions to perform 4 integer operations with one instruction
The second strategy is to use SSE2 instructions to perform 4 integer operations using a single instruction.
Here the gain will be small, but it is important, since it is applied in the calculation of the count array offset.
3rd Strategy: Unroll the larger loop of 4 iterations
And the third strategy is to do an unroll loop on the big for (which repeats 4 times).
It might seem like an unnecessary strategy, but this unroll allows us to replace multiple variables with constants in the final iteration.
Final Algorithm
// 1st optimization: calculate the counting array outside the main loop
// 2nd optimization: use SSE2
// 3rd optimization: loop unroll
#if _MSC_VER
#define _mm_i32_(v,i) (v).m128i_i32[i]
#else
#define _mm_i32_(v,i) ((int32_t*)&(v))[i]
#endif
__m128i counting[256];
memset(counting, 0, sizeof(__m128i) * 256);
// count all bytes
for (j = 0; j < N; j++){
_mm_i32_(counting[(in[j]) & 0xff], 0)++;
_mm_i32_(counting[(in[j] >> 8) & 0xff], 1)++;
_mm_i32_(counting[(in[j] >> 16) & 0xff], 2)++;
_mm_i32_(counting[(in[j] >> 24) & 0xff], 3)++;
}
//compute offsets
__m128i acc = counting[0];
counting[0] = _mm_set1_epi32(0);
for (uint32_t j = 1; j < 256; j++) {
__m128i tmp = counting[j];
counting[j] = acc;
acc = _mm_add_epi32(acc, tmp);
}
const __m128i _c_0 = _mm_setr_epi32(1, 0, 0, 0);
const __m128i _c_1 = _mm_setr_epi32(0, 1, 0, 0);
const __m128i _c_2 = _mm_setr_epi32(0, 0, 1, 0);
const __m128i _c_3 = _mm_setr_epi32(0, 0, 0, 1);
//shift = 0
{
// place elements in the output array
for (uint32_t j = 0; j < arrSize; j++) {
uint32_t currItem = in[j];
uint32_t bucket_index = ((currItem) & 0xff);
uint32_t out_index = _mm_i32_(counting[bucket_index], 0);
counting[bucket_index] = _mm_add_epi32(counting[bucket_index], _c_0);
out[out_index] = currItem;
}
//swap out, in
uint32_t* tmp = in;
in = out;
out = tmp;
}
//shift = 8
{
// place elements in the output array
for (uint32_t j = 0; j < arrSize; j++) {
uint32_t currItem = in[j];
uint32_t bucket_index = ((currItem >> 8) & 0xff);
uint32_t out_index = _mm_i32_(counting[bucket_index], 1);
counting[bucket_index] = _mm_add_epi32(counting[bucket_index], _c_1);
out[out_index] = currItem;
}
//swap out, in
uint32_t* tmp = in;
in = out;
out = tmp;
}
//shift = 16
{
// place elements in the output array
for (uint32_t j = 0; j < arrSize; j++) {
uint32_t currItem = in[j];
uint32_t bucket_index = ((currItem >> 16) & 0xff);
uint32_t out_index = _mm_i32_(counting[bucket_index], 2);
counting[bucket_index] = _mm_add_epi32(counting[bucket_index], _c_2);
out[out_index] = currItem;
}
//swap out, in
uint32_t* tmp = in;
in = out;
out = tmp;
}
//shift = 24
{
// place elements in the output array
for (uint32_t j = 0; j < arrSize; j++) {
uint32_t currItem = in[j];
uint32_t bucket_index = ((currItem >> 24) & 0xff);
uint32_t out_index = _mm_i32_(counting[bucket_index], 3);
counting[bucket_index] = _mm_add_epi32(counting[bucket_index], _c_3);
out[out_index] = currItem;
}
//swap out, in
uint32_t* tmp = in;
in = out;
out = tmp;
}
The source code is available:here.
Result
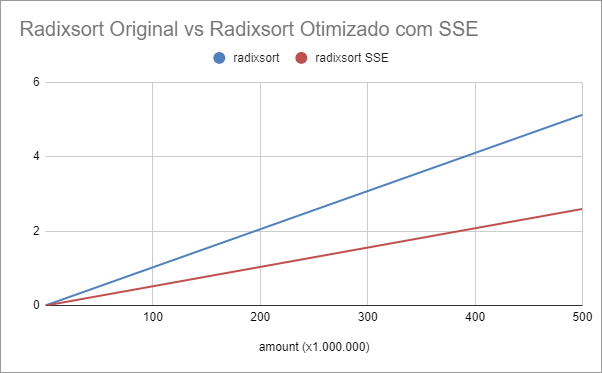
The table below shows the times of our base algorithm compared to the optimized version using SSE.
Execution Time Radixsort vs Radixsort SSE (secs)
| amount (Mega) | radixsort | radixsort SSE |
|---|---|---|
| 0,1 | 0,000999 | 0,000569 |
| 0,5 | 0,004812 | 0,002236 |
| 1 | 0,009914 | 0,004855 |
| 5 | 0,050997 | 0,024821 |
| 10 | 0,101511 | 0,050143 |
| 50 | 0,510289 | 0,255025 |
| 100 | 1,025262 | 0,499212 |
| 500 | 5,125806 | 2,598452 |
The algorithm modified with SSE, has an average speedup of 2.
See the response time in seconds comparison graph below:
Conclusion
Of the three strategies presented above, the one that has the most impact, due to the nature of the algorithm, is the elimination of traversals in the input array.
Using SSE and the unroll loop has a minor impact on the overall performance of the algorithm.
An interesting fact is that the parallel version now has a very low gain compared to our optimized version.
This reinforces the idea that the execution time of this algorithm is more influenced by movements in memory than computations in the CPU.
Hope you liked the content.
best regards,
Alessandro Ribeiro
