Programação de Personagem 3D Parte 2 de 3: Animação Esqueletal

A animação esqueletal é uma forma de dar vida, movimento, suavidade à sequências de poses utilizando transformações geométricas.

Nossa preocupação nesse post está centrada em como realizar essa transição de quadros partindo de uma pose para outra.

1 Contexto

A animação em computação gráfica é uma área vasta. Ela pode ser realizada de várias formas: geração procedural, troca de imagens/sprites que estão em uma sequência, modificação dos vértices ou de suas propriedades, ou qualquer modificação de parâmetros que afetam visualmente um objeto.

Todas elas se baseiam em modificar o visual do que é apresentado na tela considerando a variação de tempo. Então precisamos codificar de alguma forma essa variação de tempo.

Neste post vamos apresentar a animação aplicada às matrizes de transformação.

Chamamos de esqueleto a estrutura hierárquica que geralmente utilizamos para controlar o skinning de mesh (que foi o tema do nosso post anterior).

Apesar do nome desse post ser animação esqueletal, essa técnica pode ser utilizada para realizar a animação de qualquer estrutura de transformações hierárquicas.

Quando queremos criar uma animação temos a definição do que é um quadro. No nosso contexto, um quadro é todo o conjunto de parâmetros que foram criados ou calculados para nos ajudar a definir nossa pose final, ou conjunto de transformações finais.

2 Keyframes

Quando um artista está criando uma animação computadorizada, geralmente ele não trabalha em todos os quadros(frames). Ele cria quadros importantes que destacam o movimento e sua intenção.

Esse quadro importante chamamos de quadro chave ou keyframe.

Todos os outros quadros são aproximados, interpolados ou extrapolados.

Então nossa animação é composta basicamente por dois tipos de configurações de parâmetros (quadros): as que o artista definiu, e as que o artista não definiu.

Existe uma diferença entre elas que pode nos guiar nesse post.

Quando falamos de parâmetros, pensamos em curvas. Onde cada curva controla o comportamento de um parâmetro.

Quando uma curva é aproximada, ela não passa pelos pontos de controle. Quando é interpolada, ela passa pelos pontos de controle. As extrapolações podem ou não passar pelos pontos de controle, mas elas extrapolam o movimento definido.

Existem inúmeras equações para tratar cada um desses casos: linear, hermite, as famílias de splines (spline, b-spline, catmullrom-splines, etc… ), bezier, etc...

Se você quiser se aprofundar nesse mundo de equações, sugiro também procurar os livros de computação gráfica clássica.

Quando um artista cria os estados de animação, geralmente ele utiliza ferramentas mais robustas com diversas opções de interpolações. Quando ele exporta o modelo 3D para aplicações de tempo-real, essas informações complexas são transformadas em informações mais simples, para que os softwares de reprodução possam trabalhar com essas equações.

Por isso, aqui vamos nos ater ao caso mais simples, que é utilizar equações lineares para tratar as interpolações.

2.1 Como Codificar os Keyframes?

Para codificar os keyframes temos que pensar que os mesmos são conjuntos de valores associados a um determinado tempo (timestamp).

A forma mais simples seria armazenar um array de estruturas, onde teríamos um campo que indica o tempo daquele keyframe e outro campo com o nosso parâmetro (posição, rotação ou escala).

Você pode complicar o quanto quiser nessas definições. Eu já vi implementações em que são codificados um array para cada componente da posição. Um para o 'x', outro para o 'y' e outro para o 'z'. Dá mais controle sobre os parâmetros, mas no nosso caso, queremos simplificar o máximo possível.

Vamos ver um exemplo de uma animação posicional com 3 frames: um no início que define o estado inicial, um intermediário, e um final. Veja a imagem abaixo:

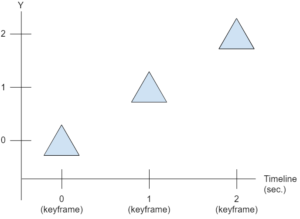
Na imagem de exemplo temos a variação representada somente para o eixo ‘Y’, mas você pode considerar que temos armazenados todos os 3 componentes de uma coordenada 3D ou 2 componentes de uma coordenada 2D. Quando representamos rotações, podemos armazenar o quatérnion de cada keyframe também.

Podemos armazenar essa sequência de keyframes usando as estruturas abaixo (em c++):

// Positional Structure
struct KeyframePos {
    float time; // seconds
    vec3 pos;
    KeyframePos(float time, const vec3 &pos) {
        this->time = time;
        this->pos = pos;
    }
};
// Rotational Structure
struct KeyframeRot {
    float time; // seconds
    quat rot;
    KeyframeRot(float time, const quat &rot) {
        this->time = time;
        this->rot = rot;
    }
};

Podemos inicializar um array que representa essa animação da seguinte forma:

std::vector<KeyframePos> channelPosition;
channelPosition.push_back( KeyframePos( 0.0f, vec3( 0, 0.0f, 0 ) ) );
channelPosition.push_back( KeyframePos( 1.0f, vec3( 0, 1.0f, 0 ) ) );
channelPosition.push_back( KeyframePos( 2.0f, vec3( 0, 2.0f, 0 ) ) );

É importante manter esse array ordenado pelo tempo para facilitar nosso algoritmo mais para frente.

Agora nossa representação dessa timeline pode ser representada com a imagem a seguir:

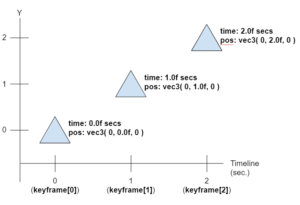
Agora que já temos uma forma de definir nossos keyframes, podemos pensar em como fazer para calcular os valores intermediários (que não foram definidos pelo artista). Assim podemos abordar as interpolações.

3 Interpolações

Uma interpolação é o cálculo de estados intermediários de parâmetros, onde esses parâmetros passam pelos pontos de controle, ou seja, eles passam pelos estados definidos pelo artista.

Vamos pegar o exemplo anterior, só que agora, estamos interessados nas posições que não foram definidas pelo artista. Veja a imagem a seguir:

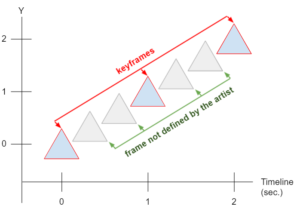
3.1 Como Calcular as Interpolações?

Para calcular uma interpolação temos que calcular qual a porcentagem que o tempo atual está em relação aos tempos dos keyframes mais próximos.

Veja a imagem a seguir:

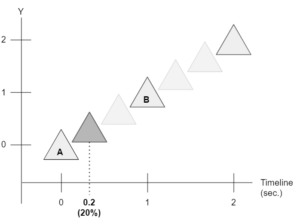
Nesse exemplo, o tempo atual da nossa simulação está a 20% (ou 0.2) em relação ao tempo de 'A' e 'B'.

Geralmente as animações podem ser codificadas para serem reproduzidas para frente ou para trás. Iremos considerar que as animações são reproduzidas somente para frente, assim podemos criar um algoritmo que calcula a porcentagem do tempo atual sobre nosso array de keyframes mais otimizado (que não precisa percorrer todo o array para encontrar a posição de interpolação).

Veja o código a seguir:

class QueryInterpolationPos {
 
public:
    void QueryInterpolationPos() {
        lastIndexA = -1;
        lastIndexB = -1;
        lastLrp = 0.0f;
        lastTimeQuery = 0.0f;
    }
 
    void queryInterval_ForwardLoop(
        const std::vector<KeyframePos> &channel, float time, 
        KeyframePos **out_A, KeyframePos **out_B, float *out_lrp ) {
 
        if (lastIndexA == -1) {
            // initialize data
            lastIndexA = 0;
            lastIndexB = 1;
            lastLrp = 0.0f;
            lastTimeQuery = channel[0].time;
        }
 
        if (channel.size() == 0) {
            *out_A = *out_B = NULL;
            *out_lrp = 0.0f;
            return;
        } else if (channel.size() == 1) {
            *out_A = *out_B = &channel[0];
            *out_lrp = 0.0f;
            return;
        }
 
        time = clamp(time, channel[0].time, channel[channel.size() - 1].time);
 
        if (time < lastTimeQuery) {
            // reset query
            lastIndexA = 0;
            lastIndexB = 1;
            lastLrp = 0.0f;
            lastTimeQuery = channel[0].time;
        }
 
        if (time > lastTimeQuery) {
            lastTimeQuery = time;
            for (; lastIndexA < channel.size() - 2; lastIndexA++) {
                if (time < channel[lastIndexA + 1].time)
                    break;
            }
            lastIndexB = lastIndexA + 1;
        } else {
            // same time query
            *out_A = &channel[lastIndexA];
            *out_B = &channel[lastIndexB];
            *out_lrp = lastLrp;
            return;
        }
 
        float delta = (channel[lastIndexB].time - channel[lastIndexA].time);
 
        if (delta <= 1.0e-6)
            lastLrp = 0.0f;
        else
            lastLrp = (time - channel[lastIndexA].time) / delta;
 
        *out_A = &channel[lastIndexA];
        *out_B = &channel[lastIndexB];
        *out_lrp = lastLrp;
    }
};

O código apresentado mostra como procurar os keyframes de posição, mas a lógica para procurar por rotações é a mesma, só trocando o tipo KeyframePos por KeyframeRot.

Uma vez que temos o keyframe A (out_A), o keyframe B (out_B) e a porcentagem que o tempo atual está em relação a estes (out_lrp), podemos pensar em qual equação utilizar na interpolação.

Existem dois tipos de interpolação: a interpolação posicional e a interpolação rotacional.

Não é usual realizar interpolações de escala, mas você pode considerar também essa possibilidade.

3.2 Interpolação Posicional

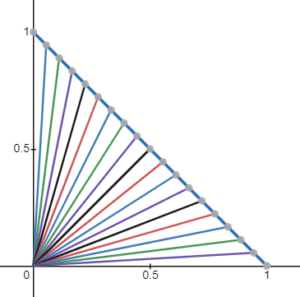
O ponto chave da interpolação posicional é manter a variação de distância constante, mesmo que isso possa não gerar variações de ângulos constantes.

Para a interpolação posicional, podemos utilizar a interpolação linear. O resultado que obtemos com essa interpolação é a movimentação realizada em linhas retas que ligam os pontos das posições definidas nos keyframes.

Geralmente não é necessário se preocupar se os valores interpolados se aproximam ou não do movimento criado pelo artista, porque as ferramentas de exportação fazem uma amostragem grande do movimento que foi criado (bake de animação), fazendo com que esses valores se aproximem ao máximo da curva original.

Veja o algoritmo abaixo:

vec3 lerp(const vec3 &a, const  vec3 &b, float factor) {
    return a * (1.0f - factor) + (b*factor);
}

Imagine que o movimento desejado pelo artista é fazer o caminhamento sobre um arco, mas ao exportar para utilizar a interpolação linear, temos esse resultado:

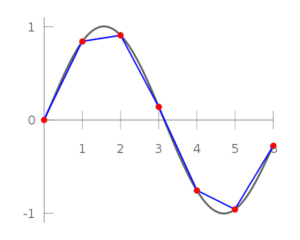
A linha cinza é o movimento desejado. A linha azul é o resultado da interpolação linear.

Geralmente essa diferença entre as interpolações não é perceptível.

3.3 Interpolação Rotacional

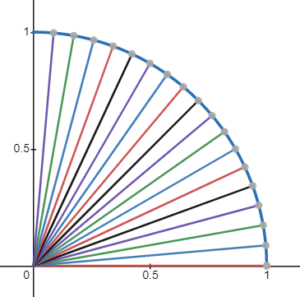
O ponto chave da interpolação rotacional é manter a variação de ângulo constante ao invés de manter a variação de distância constante. Outro ponto importante é que as posições geradas por essa interpolação seguem a silhueta de um círculo, mantendo a distância até o centro de rotação constante.

Para esse tipo de interpolação podemos falar em quaternions.

Até o momento nós falamos em construir nosso arcabouço de transformações somente com matrizes.

Agora falamos de quaternions, porque é uma outra estrutura matemática que nos ajuda a obter bons resultados com um baixo custo computacional.

3.3.1 Quaternions

Um quaternion é uma estrutura matemática com 4 valores, sendo 3 coordenadas no espaço complexo (com números imaginários) onde podemos codificar rotações e escalas. Em computação gráfica geralmente ele é utilizado para representar somente rotações.

Os quatérnions são mais interessantes que matrizes para representar rotações porque eles evitam um fenômeno chamado gimbal-lock, que pode ocorrer quando você trata as rotações utilizando somente matrizes.

O gimbal-lock é um estado de composição de rotações (exemplo: rotação de Euler) em que 2 ou mais eixos de rotação estão alinhados. Quando isso ocorre, podem ocorrer 2 problemas:

• a rotação desses 2 eixos resultam na mesma rotação final;
• a interpolação de 2 rotações podem gerar um arco que não ‘caminha’ no arco mínimo de uma rotação de origem até a rotação alvo.

A questão mais chata para se trabalhar com os quatérnions são as operações que podem ser realizadas sobre eles, uma vez que o espaço de coordenadas é o espaço complexo.

As operações que considero importantes estão relacionadas a:

• criar uma rotação a partir de parâmetros conhecidos (ex.: rotações de Euler);
• transformar essa representação em uma matriz para usarmos no nosso sistema de renderização.

Para a nossa alegria, muitos livros trazem implementações de operações com quatérnions, então precisamos saber o que elas fazem para poder utilizá-las.

3.3.2 Equações e Algoritmo

Nossos keyframes de rotações agora serão armazenados em quatérnios e a operação principal que utilizaremos é o SLERP (spherical linear interpolation).

O SLERP realiza a variação constante de ângulos de um quatérnion de origem para um quaternion alvo.

A forma de utilizar ele se parece com a interpolação linear. Temos um quaternion ‘a’ de origem, um quaternion ‘b’ de destino e um fator de 0 a 1 que fala qual a porcentagem que desejamos realizar a rotação que vai de ‘a’ até ‘b’.

Veja o algoritmo abaixo:

quat slerp(const quat& a, const quat& b, float lerp) {
    if (lerp <= 0.0f) return a;
    if (lerp >= 1.0f) return b;
 
    float _cos = dot(a, b);
    quat _new_b_(b);
    if (_cos < 0.0f) {
        _new_b_ = -b;
        _cos = -_cos;
    }
    float a_factor, b_factor;
    if (_cos > (1.0f - EPSILON)) {
        a_factor = 1.0f - lerp;
        b_factor = lerp;
    } else {
        float _sin = sqrt(1.0f - _cos * _cos);
        float _angle_rad = atan2(_sin, _cos);
        float _1_over_sin = 1.0f / _sin;
        a_factor = sin((1.0f - lerp) * _angle_rad) * _1_over_sin;
        b_factor = sin((lerp)* _angle_rad) * _1_over_sin;
    }
    return a_factor * a + b_factor * _new_b_;
}

É possível implementar esse tipo de interpolação com vetores também, veja o algoritmo abaixo:

vec3 slerp(const vec3& a, const vec3& b, float lerp) {
    float _cos = clamp(dot(normalize(a), normalize(b)), -1.0f, 1.0f);
    float angle_rad = acos(_cos);
    float _sin = sin(angle_rad);
    if (abs(_sin) < EPSILON)
        return aRibeiro::lerp(a, b, lerp);
    float a_factor = sin((1.0f - lerp) * angle_rad) / _sin;
    float b_factor = sin(lerp * angle_rad) / _sin;
    return a * a_factor + b * b_factor;
}

Não é comum utilizar um vec3 para representar rotações, mas essa função pode ser útil em outras situações.

3.4 Comparando as Interpolações

Quando colocamos o resultado sobreposto das interpolações, podemos ver que elas geram resultados diferentes.

Veja a imagem abaixo:

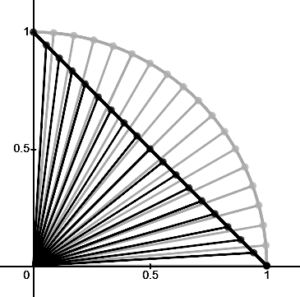
A trajetória da interpolação rotacional segue o arco do círculo, enquanto a interpolação posicional segue em linha reta.

Uma das questões no post anterior que foi levantada é que a interpolação utilizada como exemplo é somente linear.

Com a imagem acima é possível ver que quando usamos uma interpolação linear, a mesma não mantém o mesmo passo angular, que é a premissa da interpolação rotacional. No caso do mesh skinning, o resultado pode ficar ruim, dependendo de como os parâmetros são interpolados. Mas na maior parte dos casos, não é perceptível.

3.5 Exemplo de Utilização de Interpolação

Agora que sabemos como fazer as interpolações, podemos usar nosso algoritmo que procura por keyframes e utilizar o seu resultado tanto na interpolação posicional quanto na rotacional.

Veja o exemplo abaixo:

void example_query_position() {
    std::vector<KeyframePos> channelPosition;
    QueryInterpolationPos queryInterpolationPos;
 
    //initialize the position channel
    //...
 
    KeyframePos *out_A, *out_B;
    float out_lrp;
 
    //query time 0.2 in the timeline
    queryInterpolationPos.queryInterval_ForwardLoop( 
        &channelPosition, 0.2f, // vector, seconds
        &out_A, &out_B, &out_lrp // output parameters
    );
 
    //check if found a keyframe
    if (out_A == NULL)
        return;
 
    //now we can compute our interpolation
    vec3 result = lerp( out_A->pos, out_B->pos, out_lrp);
}

Para a rotação, o código é similar. Apenas precisamos trocar o lerp pelo slerp, e utilizar quaternions ao invés de vec3.

4 Conjunto de Canais de Animação

Um canal de animação pode ser definido como uma interpolação (posicional ou rotacional) aplicada diretamente a um array de parâmetros (posição, rotação ou escala) considerando uma timeline.

Nós estamos interessados em uma definição mais completa que possa ser aplicada diretamente a um nó na nossa hierarquia de transformações. Para isso, podemos juntar um conjunto de atributos e falar que esse vai ser nosso conjunto de canais de animação que representam nossa transformação.

Esse conjunto pode utilizar a interpolação linear para a posição e escala, e a interpolação rotacional para a rotação.

Sabendo que as estruturas de interpolação funcionam da mesma forma (com o mesmo parâmetro de porcentagem), podemos criar uma classe de controle que calcula cada um desses parâmetros e retorna para nós uma única matriz com o resultado de todas as interpolações combinadas.

Veja um exemplo da definição da classe de transformação:

class TransformAnimation {
public:
    std::vector<KeyframePos> channelPosition;
    QueryInterpolationPos queryInterpolationPos;
    std::vector<KeyframeRot> channelRotation;
    QueryInterpolationRot queryInterpolationRot;
 
    vec3 queryPosition(float time) {
        KeyframePos *out_A, *out_B;
        float out_lrp;
        queryInterpolationPos.queryInterval_ForwardLoop( 
            &channelPosition, time, // vector, seconds
            &out_A, &out_B, &out_lrp // output parameters
        );
        if (out_A == NULL)
            return vec3(0);
        return lerp( out_A->pos, out_B->pos, out_lrp);
    }
 
    quat queryRotation(float time) {
        KeyframeRot *out_A, *out_B;
        float out_lrp;
        queryInterpolationRot.queryInterval_ForwardLoop( 
            &channelRotation, time, // vector, seconds
            &out_A, &out_B, &out_lrp // output parameters
        );
        if (out_A == NULL)
            return quat(0,0,0,1);
        return slerp( out_A->rot, out_B->rot, out_lrp);
    }
 
    mat4 computeMatrix(float time) {
        vec3 pos = queryPosition(time);
        quat rot = queryRotation(time);
        return translateMatrix(pos) * quat2Mat4(rot);
    }
};

Como você pode ver no código, precisamos passar somente o tempo atual para o controlador de transformação. Internamente ele já combina os diferentes tipos de parâmetros que temos na matriz final, para que possamos utilizar na nossa renderização.

4.1 Cinemática Inversa/Direta

Outra questão que surge quando tratamos as animações é qual o tipo de cinemática que vamos utilizar.

Na cinemática direta você tem um conjunto de ângulos associados aos nós de transformação e no final é calculada a posição final de cada nó.

Veja a equação abaixo:

P = f(Θ)

Na cinemática inversa você tem um conjunto de posições finais, e um algoritmo de resolução de equações simultâneas calcula qual a configuração de ângulos é necessária atribuir a cada nó para atingir essas posições finais.

Veja a equação abaixo:

Θ = f^-1(P)

Geralmente os editores utilizam a cinemática inversa para facilitar o controle sobre a animação. Mas isso tem um custo computacional elevado. Tão elevado, que as aplicações de tempo-real, quando usam essa abordagem, aplicam somente para os pés do personagem, e não para o corpo inteiro.

Em contrapartida, após a exportação da animação, os softwares utilizam a cinemática direta.

A principal vantagem da cinemática direta é que o cálculo das posições dos nós de transformação pode ser realizado com uma simples multiplicação de matriz. Ou seja, ela é computacionalmente mais leve que a cinemática inversa.

Lembra como fazemos para calcular a matriz final de uma hierarquia de transformações do nosso post anterior?

Pois é, para calcular a cinemática direta, nós temos que fazer exatamente o mesmo. Basta multiplicar a matriz do nó pai pela matriz do nó filho.

Uma vantagem dessa abordagem é que podemos armazenar os valores da animação no espaço local de cada nó da hierarquia.

Com essas definições, já podemos criar nossa animação.

A cada amostra de tempo em nossa timeline faremos o cálculo da interpolação necessária.

Isso nos leva a ter a definição da nossa pose interpolada do nosso esqueleto.

No exemplo abaixo podemos ver os quadros chave e os frames interpolados:

O algorítmo para utilizar esse tipo de animação fica da seguinte forma:

Para cada amostra de tempo ‘time’:
    1 Para cada transformação ‘transform’
        transform ← transformAnimation.computeMatrix( time )
    2 Calcular matriz final (multiplicar todas as matrizes da hierarquia)
    3 Enviar conjunto de matrizes final para renderizar o modelo 3D
        Aqui pode utilizar para computar o skinning ou enviar para o shader

5 Transições

Vamos considerar agora que uma animação é o conjunto de canais dos parâmetros de todos os nós de um personagem. Vamos considerar também que esse personagem pode ter várias animações.

Quando queremos fazer a troca de uma animação para outra podemos usar uma transição.

Uma transição é um estado intermediário entre duas animações.

A ideia por trás da implementação de uma transição é muito simples:

1. Calcular todas as interpolações dos parâmetros da animação ‘1’ e animação ‘2’;
2. Combinar os resultados dos parâmetros da animação ‘1’ com a animação ‘2’ utilizando um parâmetro ‘lrp’;
3. Criar a matriz final de transformação a partir do resultado anterior.

5.1 Algoritmo

Considere três parâmetros:

• ‘lrp’ como o parâmetro de interpolação entre as animações (0 à 1);
• ‘time_a’ o tempo atual da animação ‘1’;
• ‘time_b’ o tempo atual da animação ‘2’.

Precisamos fazer 2 tipos de processamento: um que processa os canais que são independentes e outro que processa os canais compartilhados.

Obs.: Um canal compartilhado é um canal de animação que é alterado tanto na animação ‘1’ quanto na animação ‘2’.

A lógica do processamento dos canais independentes funciona como descrito anteriormente.

Agora nos canais compartilhados podemos utilizar o algoritmo a seguir:

Para cada canal compartilhado ‘a’ da animação ‘1’:
    ‘b’ ← encontre o canal da animação ‘2’ que compartilha a mesma transformação de ‘a’
    a_pos ← ‘a’.queryPosition( time_a )
    b_pos ← ‘b’.queryPosition( time_b )
    result_pos ← lerp( a_pos, b_pos,  lrp )
    a_rotation ← ‘a’.queryRotation( time_a )
    b_rotation ← ‘b’.queryRotation( time_b )
    result_rotation ← slerp( a_rotation, b_rotation,  lrp )
    result_matrix ← translate( result_pos ) * quat2Mat4( result_rotation )

Com esse algoritmo podemos aplicar a transição de animações a qualquer estrutura de transformações hierárquica.

A combinação de poses pode levar a resultados visuais estranhos, mas esses resultados dependem de como o artista criou as curvas de animação e também de como o programador definiu os algoritmos de blending.

6 Conclusão

Esse post é o segundo de três, onde pretendemos abordar o controle de movimentação de personagem 3D.

Podemos utilizar o resultado do processamento da animação esqueletal para definir a target_pose do nosso skinning de mesh (lembrando do post anterior).

Essa técnica pode ser aplicada também à hierarquia de cena (não necessariamente a um personagem).

O próximo post será sobre o movimento sobre o nó raiz. Não deixe de acompanhar nossas publicações.

Obrigado por ler esse post.

Um abraço,

Alessandro Ribeiro