O problema de ordenação é tratado como um problema básico.
Geralmente estudamos esse tópico quando estamos dando nossos primeiros passos no mundo da programação.
Venho através desse post revisar essa questão com o enfoque prático relacionado a ordenação de números usando o algoritmo do radixsort, bucketsort e countingsort.
1. Complexidade de Algoritmos de Ordenação Conhecidos
Os algoritmos de ordenação mais simples costumam ter complexidade O(n²).
E os algoritmos mais trabalhados podem chegar a ter a complexidade O(n log n).
Abaixo tem uma relação de algoritmos e suas respectivas complexidades:
- Bubble Sort: O(n²)
- Heap Sort: (n log n)
- Insertion Sort: O(n²)
- Mergesort: O(n log n)
- Selection Sort: O(n²)
- Shellsort: O(n²)
- Quicksort: O(n log n) à O(n²)
Abaixo a lista dos algoritmos que vamos abordar nesse post:
- Bucket Sort: O(n)
- Counting Sort: O(n)
- Radix Sort: O(n)
2. Casos Especiais
O Bucket Sort, o Counting Sort e o Radix Sort foram feitos para ordenar números.
Nenhum deles utiliza comparações para funcionar.
2.1. Bucket Sort e Counting Sort
O bucket sort é bastante semelhante ao counting sort.
Estes algoritmos consideram que todos os elementos já sabem qual é a posição que devem ocupar na ordenação.
Basta agora identificar essas posições e no final realizar a movimentação para o array de saída ordenado.
Bucket Sort
O bucket sort precisa que você aloque uma lista para cada número do conjunto que você está ordenando, essa lista é chamada de bucket (balde).
Quando você for percorrer o array, precisa colocar o valor no respectivo bucket.
Por fim, basta percorrer todos os seus buckets que o resultado estará ordenado.
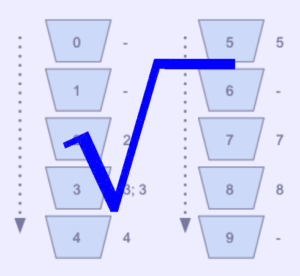
Vamos considerar a sequência: 7453283
Cada número deve ser colocado no seu respectivo bucket.
Veja a imagem abaixo de exemplo:
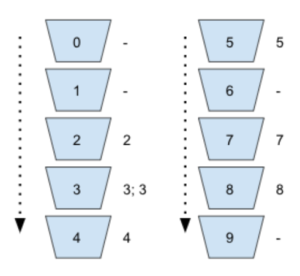
Quando percorremos os buckets que já estão em ordem, temos o nosso array ordenado: 2334578
Counting Sort
O counting sort é uma variação desse método, mas que não precisa de uma lista armazenada para cada posição para ordenar.
Você percorre seu vetor uma vez para saber quantos elementos tem em cada posição.
É necessário calcular o offset de cada elemento que você está contando.
Depois disso você pode percorrer o array mais uma vez para já colocar os elementos no offset correto.
Exemplo:
entrada: 7453283
* 1 passo -> contar os elementos
**********
Contagem:
0 1 2 3 4 5 6 7 8 9
|0|0|1|2|1|1|0|1|1|0|
* 2 passo -> calcular os offsets, pode-se usar
********** o mesmo array de contagem para isso
Utilizamos o algoritmo:
uint32_t acc = 0;
for (uint32_t j = 0; j < max_bucket_symbols; j++) {
counter_type tmp = counting[j];
offset[j] = acc;
acc += tmp;
}
Contagem:
0 1 2 3 4 5 6 7 8 9
|0|0|1|2|1|1|0|1|1|0|
Offset:
0 1 2 3 4 5 6 7 8 9
|0|0|0|1|3|4|5|5|6|7|
* 3 passo -> posicionar os elementos ordenados no vetor de saída
**********
entrada: 7453283
→ elemento: 7
-------------
Offset:
+1
↓
0 1 2 3 4 5 6 7 8 9
|0|0|0|1|3|4|5|5|6|7|
↓
6
Saida:
0 1 2 3 4 5 6
| | | | | |7| |
↑
→ elemento: 4
-------------
Offset:
+1
↓
0 1 2 3 4 5 6 7 8 9
|0|0|0|1|3|4|5|6|6|7|
↓
4
Saida:
0 1 2 3 4 5 6
| | | |4| |7| |
↑
→ elemento: 5
-------------
Offset:
+1
↓
0 1 2 3 4 5 6 7 8 9
|0|0|0|1|4|4|5|6|6|7|
↓
5
Saida:
0 1 2 3 4 5 6
| | | |4|5|7| |
↑
→ elemento: 3
-------------
Offset:
+1
↓
0 1 2 3 4 5 6 7 8 9
|0|0|0|1|4|5|5|6|6|7|
↓
2
Saida:
0 1 2 3 4 5 6
| |3| |4|5|7| |
↑
→ elemento: 2
-------------
Offset:
+1
↓
0 1 2 3 4 5 6 7 8 9
|0|0|0|2|4|5|5|6|6|7|
↓
1
Saida:
0 1 2 3 4 5 6
|2|3| |4|5|7| |
↑
→ elemento: 8
-------------
Offset:
+1
↓
0 1 2 3 4 5 6 7 8 9
|0|0|1|2|4|5|5|6|6|7|
↓
7
Saida:
0 1 2 3 4 5 6
|2|3| |4|5|7|8|
↑
→ elemento: 3
-------------
Offset:
+1
↓
0 1 2 3 4 5 6 7 8 9
|0|0|1|2|4|5|5|6|7|7|
↓
3
Saida:
0 1 2 3 4 5 6
|2|3|3|4|5|7|8|
↑
Uma questão que deve ser observada nos dois algoritmos é que o array contendo os elementos tanto no bucket sort quanto na counting sort precisa ter uma quantidade de slots igual ao total de símbolos do conjunto de entrada.
Se você tem um inteiro de 32 bits, precisará de 4.294.967.295 posições para que ambos os algoritmos funcionem.
2.2. Radix Sort
O radix sort se baseia em filtrar um dígito, ordená-lo, e filtrar o dígito seguinte até o número ou string estarem ordenados.
Ele não fala como você vai ordenar cada dígito, apenas fala que você precisa realizar esse filtro.
A ordem de filtragem é do dígito menos significativo para o mais significativo.
Veja o exemplo:
Entrada: 123, 542, 320 * ordenação pelo 1º dígito: 12[3], 54[2], 32[0] -> 32[0], 54[2], 12[3] * ordenação pelo 2º dígito: 3[2]0, 5[4]2, 1[2]3 -> 3[2]0, 1[2]3, 5[4]2 * ordenação pelo 3º dígito: [3]20, [1]23, [5]42 -> [1]23, [3]20, [5]42 resultado: 123, 320, 542
A complexidade deste algoritmo cresce quando o número de dígitos cresce.
Para um inteiro de 32bits, teremos 10 casas decimais (4.294.967.295), portanto a complexidade será O(kn), onde k é o número de casas decimais e n o número de elementos.
3. Misturando os Algoritmos
É comum usar o radix sort junto do bucket sort ou o counting sort.
Dessa forma o radix sort divide o trabalho, e o bucket sort ou o counting sort ordena os dígitos.
O counting sort, apesar de ser mais complexo que o bucket sort, é mais interessante porque não precisa de armazenar as listas para cada posição de ordenação.
No exemplo do radix sort, se usarmos o counting sort para cada dígito, bastaria um array de contagem/offset com 10 posições (1 para cada símbolo do conjunto que queremos ordenar).
3.1. A implementação eficiente
Vamos usar uma base que seja potência inteira de 2, porque o computador trabalha melhor na base binária e podemos utilizar shift e ands para filtrar os bits durante o processamento.
Nossa base será 256 (8bits). Isso fará que o counting sort tenha um array de contagem/offset de 256 posições.
E esse é o algoritmo final:
void radix_counting_sort_unsigned(uint32_t* _arr, uint32_t arrSize, uint32_t* tmp_array) {
if (arrSize == 0)
return;
// best performance on 8 bit of symbols...
const int32_t base_bits = 8;//1 byte
const int32_t max_bucket_symbols = 1 << base_bits;//256
const int32_t base_mask = max_bucket_symbols - 1;//0xff
const int32_t int_total_bytes = sizeof(uint32_t);
const uint32_t int_mask_bits = 0xffffffff;
const int32_t int_total_bits = int_total_bytes << 3;// *8;
const int32_t radix_num = (int_total_bits / base_bits) +
((int_total_bits % base_bits) ? 1 : 0);
const uint32_t last_radix_mask = int_mask_bits >>
((radix_num - 1) * base_bits);
int32_t shift = 0;
//Counting Sort
counter_type counting[max_bucket_symbols];
uint32_t* aux;
if (tmp_array == NULL)
aux = (uint32_t*)malloc_aligned(arrSize * sizeof(uint32_t));
else
aux = tmp_array;
uint32_t* in = _arr;
uint32_t* out = aux;
for (int32_t i = 0; i < radix_num; i++) {
// Cleaning counters
memset(counting, 0, sizeof(counter_type) * max_bucket_symbols);
// count the elements
for (uint32_t j = 0; j < arrSize; j++) {
uint32_t currItem = in[j];
uint32_t bucket_index = (((uint32_t)currItem >>
shift) & base_mask);//0xff
counting[bucket_index]++;
}
//compute offsets
counter_type acc = 0;
for (uint32_t j = 0; j < max_bucket_symbols; j++) {
counter_type tmp = counting[j];
counting[j] = acc;
acc += tmp;
}
// place elements in the output array
for (uint32_t j = 0; j < arrSize; j++) {
uint32_t currItem = in[j];
uint32_t bucket_index = (((uint32_t)currItem >>
shift) & base_mask);//0xff
counter_type out_index = counting[bucket_index];
counting[bucket_index]++;
out[out_index] = currItem;
}
//swap out, in
uint32_t* tmp = in;
in = out;
out = tmp;
// Change shift value for next iterations
shift += base_bits;
}
if (in != _arr)
memcpy(_arr, in, arrSize * sizeof(uint32_t));
if (tmp_array == NULL)
free_aligned(aux);
}
Você pode encontrar o código fonte atualizado: neste link.
O custo de ordenação desse algoritmo é O(4n) para inteiros de 32 bits.
É necessário percorrer o array de entrada 4 vezes para filtrar os 4 bytes dos inteiros que estamos ordenando.
Observação: Este algoritmo não usa branch para ordenar os números!
4. Resultados
Foram comparadas as implementações:
- std::sort
- mergesort do livro Algoritmos do Cormen
- Nosso radixsort otimizado
- Variação do radixsort para usar multithread
Foram testadas em 2 CPUs
- Intel Core i5-2415M
- freqüência: 2.3GHz
- núcleos/threads: 2/4
- cache
- L1: 64K (per core)
- L2: 256K (per core)
- L3: 3MB (shared)
- OS: MacOSX Catalina
- AMD Ryzen 7 5700X:
- freqüência: 3.4GHz a 4.6GHz
- núcleos/threads: 8/16
- cache
- L1: 64K (per core)
- L2: 512K (per core)
- L3: 32MB (shared)
- OS: Windows 11
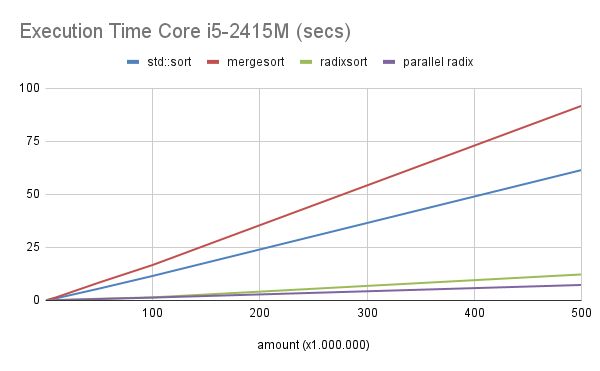
Execution Time Core i5-2415M (secs)
| amount (Mega) | std::sort | mergesort | radixsort | parallel radix |
|---|---|---|---|---|
| 0,1 | 0,00859 | 0,011625 | 0,001792 | 0,00314 |
| 0,5 | 0,047326 | 0,056289 | 0,008077 | 0,006643 |
| 1 | 0,094156 | 0,141766 | 0,016477 | 0,013934 |
| 5 | 0,496428 | 0,730969 | 0,097043 | 0,058909 |
| 10 | 1,002387 | 1,466769 | 0,190554 | 0,120432 |
| 50 | 5,577532 | 8,423516 | 0,819284 | 0,669023 |
| 100 | 11,55444 | 16,711819 | 1,453791 | 1,351016 |
| 500 | 61,453808 | 91,720573 | 12,25717 | 7,295864 |
No Core i5, comparando a versão single thread com o std::sort, o algoritmo radixsort fica com o speedup em torno de 5.
Já na versão paralela (parallel radix), comparando com o std::sort, o speedup fica em torno de 8. Exceto o primeiro caso com 100.000 números, que ficou com 2,7.
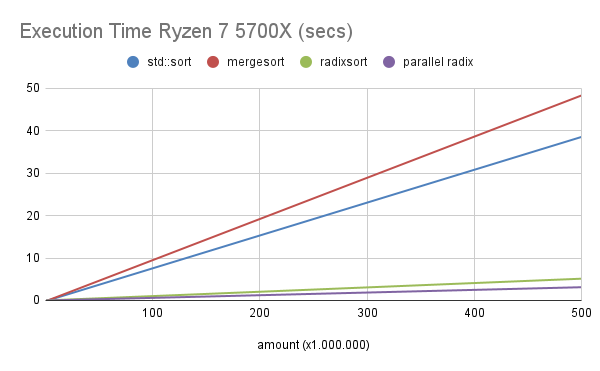
Execution Time Ryzen 7 5700X (secs)
| amount (Mega) | std::sort | mergesort | radixsort | parallel radix |
|---|---|---|---|---|
| 0,1 | 0,004388 | 0,006018 | 0,000999 | 0,000779 |
| 0,5 | 0,02543 | 0,033821 | 0,004812 | 0,002817 |
| 1 | 0,053115 | 0,070211 | 0,009914 | 0,005108 |
| 5 | 0,298237 | 0,385438 | 0,050997 | 0,0224 |
| 10 | 0,616527 | 0,800266 | 0,101511 | 0,04485 |
| 50 | 3,442063 | 4,321374 | 0,510289 | 0,228431 |
| 100 | 7,127363 | 8,943944 | 1,025262 | 0,581957 |
| 500 | 38,642517 | 48,442616 | 5,125806 | 3,129168 |
No Ryzen 7, comparando a versão single thread com o std::sort, o algoritmo radixsort fica com o speedup variando de 4,4 à 7,5 de forma crescente de acordo com a entrada.
Já na versão paralela (parallel radix), comparando com o std::sort, o speedup varia de 5,6 a 15.
Veja os gráficos abaixo:
5. Discussão dos Resultados
Em todos os sistemas testados foram observados ganhos usando o algoritmo do radixsort, e com uma certa otimização na versão paralela do mesmo.
Na execução singlethread o sistema Ryzen 7 apresentou um speedup maior devido a sua quantidade maior de memória cache L2 e L3, em relação ao sistema Core i5.
Na execução multithread o sistema Ryzen 7 apresentou um speedup maior devido a sua quantidade maior de núcleos/threads e também devido à quantidade maior de memória cache L2 e L3, em relação ao sistema Core i5.
6. Conclusão
Uma questão que foi levantada é que como não utilizamos comparações para ordenar os números, o custo de CPU desse algoritmo acaba sendo mais as operações de filtragem do radix sort (shift, and) e a contagem do counting sort.
Como geralmente operações de ALU de bits são as mais otimizadas em uma CPUs (gastam menos ciclos), me faz acreditar que outro fator, não abordado neste post, que pode estar interferindo nos nossos tempos é a velocidade de transferência do barramento de memória, pois o algoritmo precisa percorrer e gravar o array de entrada 4 vezes para gerar o resultado final.
Essa observação se torna factível, quando observamos que os speedups do Ryzen 7 são maiores que os do Core i5, tanto no single thread quando no multi thread. Considerando que uma das diferenças entre os dois é a quantidade de memória cache L2 e L3.
Essa solução apresentada serve para ordenar somente números inteiros. Se você quiser aplica-la a números de ponto flutuante, precisa usar o algoritmo abaixo para converter a representação binária do mesmo de forma que a ordenação continue funcionando:
static uint32_t sort_float_to_uint32(const float &_f) {
uint32_t f = *(uint32_t*)&_f;
uint32_t mask = (-int32_t(f >> 31)) | 0x80000000;
return f ^ mask;
}
Para os casos onde é necessário uma comparação mais complexa para a ordenação, você deverá utilizar outro algoritmo clássico. Nesse caso a melhor complexidade que costumamos ter é de O(n log n).
Espero que tenham gostado do conteúdo.
abraços,
Alessandro Ribeiro
