The sorting problem is treated as a basic problem.
We usually study this topic when we are taking our first steps in the world of programming.
I come through this post to review this issue with a practical approach related to sort numbers using the radixsort, bucketsort and countingsort algorithm.
1. Complexity of Known Sorting Algorithms
The simplest sorting algorithms usually have O(n²) complexity.
The more complex algorithms can reach O(n log n) complexity.
Below is a list of algorithms and their respective complexities:
- Bubble Sort: O(n²)
- Heap Sort: (n log n)
- Insertion Sort: O(n²)
- Mergesort: O(n log n)
- Selection Sort: O(n²)
- Shellsort: O(n²)
- Quicksort: O(n log n) to O(n²)
Below is the list of algorithms that we will cover in this post:
- Bucket Sort: O(n)
- Counting Sort: O(n)
- Radix Sort: O(n)
2. Special Cases
Bucket Sort, Counting Sort and Radix Sort were made for sorting numbers.
None of them use comparisons to work.
2.1. Bucket Sort and Counting Sort
Bucket sort is very similar to counting sort.
These algorithms assume that all elements already know which position they should occupy in the sorting.
Now we need to identify these positions and, at the end, move the elements to the sorted output array.
Bucket Sort
Bucket sort needs you to allocate a list for each number in the set you are sorting, this list is called a bucket.
When you iterate through the array, you need to put the value in the respective bucket.
Finally, just go through all your buckets and the result will be sorted.
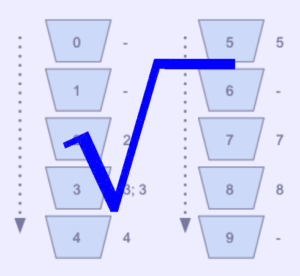
Let's consider the sequence: 7453283
Each number must be placed in its respective bucket.
See the image below for an example:
When we loop through the buckets that are already sorted, we get our sorted array: 2334578
Counting Sort
Counting sort is a variation of this method, but it does not need a stored list for each position to sort.
You traverse your array once to see how many elements you have at each position.
It is necessary to calculate the offset of each element you are counting.
After that you can loop through the array one more time to get the elements at the correct offset.
Example:
input: 7453283
* 1 step -> count elements
**********
Counting:
0 1 2 3 4 5 6 7 8 9
|0|0|1|2|1|1|0|1|1|0|
* 2 step -> calculate offsets, can use the same
********** counting array
We can use the following algorithm:
uint32_t acc = 0;
for (uint32_t j = 0; j < max_bucket_symbols; j++) {
counter_type tmp = counting[j];
offset[j] = acc;
acc += tmp;
}
Counting:
0 1 2 3 4 5 6 7 8 9
|0|0|1|2|1|1|0|1|1|0|
Offset:
0 1 2 3 4 5 6 7 8 9
|0|0|0|1|3|4|5|5|6|7|
* 3 step -> positioning the elements in the sorted output
**********
input: 7453283
→ element: 7
-------------
Offset:
+1
↓
0 1 2 3 4 5 6 7 8 9
|0|0|0|1|3|4|5|5|6|7|
↓
6
Output:
0 1 2 3 4 5 6
| | | | | |7| |
↑
→ element: 4
-------------
Offset:
+1
↓
0 1 2 3 4 5 6 7 8 9
|0|0|0|1|3|4|5|6|6|7|
↓
4
Output:
0 1 2 3 4 5 6
| | | |4| |7| |
↑
→ element: 5
-------------
Offset:
+1
↓
0 1 2 3 4 5 6 7 8 9
|0|0|0|1|4|4|5|6|6|7|
↓
5
Output:
0 1 2 3 4 5 6
| | | |4|5|7| |
↑
→ element: 3
-------------
Offset:
+1
↓
0 1 2 3 4 5 6 7 8 9
|0|0|0|1|4|5|5|6|6|7|
↓
2
Output:
0 1 2 3 4 5 6
| |3| |4|5|7| |
↑
→ element: 2
-------------
Offset:
+1
↓
0 1 2 3 4 5 6 7 8 9
|0|0|0|2|4|5|5|6|6|7|
↓
1
Output:
0 1 2 3 4 5 6
|2|3| |4|5|7| |
↑
→ element: 8
-------------
Offset:
+1
↓
0 1 2 3 4 5 6 7 8 9
|0|0|1|2|4|5|5|6|6|7|
↓
7
Output:
0 1 2 3 4 5 6
|2|3| |4|5|7|8|
↑
→ element: 3
-------------
Offset:
+1
↓
0 1 2 3 4 5 6 7 8 9
|0|0|1|2|4|5|5|6|7|7|
↓
3
Output:
0 1 2 3 4 5 6
|2|3|3|4|5|7|8|
↑
One issue that should be noted in both algorithms is that the array containing the elements in both the bucket sort and the counting sort needs to have a number of slots equal to the total number of symbols for the input set.
If you have a 32-bit integer, you'll need 4,294,967,295 positions for both algorithms to work.
2.2. Radix Sort
Radix sort is based on filtering a digit, sorting it, and filtering the next digit until the number or string is sorted.
It doesn't say how you are going to order each digit, it just says that you need to perform this filter.
The filtering order is from the least significant digit to the most significant.
See the example:
Input: 123, 542, 320 * sorting the 1st digit: 12[3], 54[2], 32[0] -> 32[0], 54[2], 12[3] * sorting the 2nd digit: 3[2]0, 5[4]2, 1[2]3 -> 3[2]0, 1[2]3, 5[4]2 * sorting the 3rd digit: [3]20, [1]23, [5]42 -> [1]23, [3]20, [5]42 result: 123, 320, 542
The complexity of this algorithm grows as the number of digits grows.
For a 32-bit integer, we will have 10 decimal places (4,294,967,295), so the complexity will be O(kn), where k is the number of decimal places and n the number of elements in the array.
3. Combining the Algorithms
It is common to use radix sort together with bucket sort or counting sort.
In this way the radix sort divides the work, and the bucket sort or counting sort sorts the digits.
Counting sort, despite being more complex than bucket sort, is more interesting because it doesn't need to store the lists for each sorting position.
In the radix sort example, if we use counting sort for each digit, the count/offset array will have 10 positions (1 for each symbol in the set we want to sort).
3.1. The efficient implementation
Let's use a base that is an integer power of 2, because the computer works best in binary base and we can use SHIFT and ANDs to filter the bits during processing.
Our base will be 256 (8bits). This will make the counting sort have a counting/offset array of 256 positions.
This is the final algorithm:
void radix_counting_sort_unsigned(uint32_t* _arr, uint32_t arrSize, uint32_t* tmp_array) {
if (arrSize == 0)
return;
// best performance on 8 bit of symbols...
const int32_t base_bits = 8;//1 byte
const int32_t max_bucket_symbols = 1 << base_bits;//256
const int32_t base_mask = max_bucket_symbols - 1;//0xff
const int32_t int_total_bytes = sizeof(uint32_t);
const uint32_t int_mask_bits = 0xffffffff;
const int32_t int_total_bits = int_total_bytes << 3;// *8;
const int32_t radix_num = (int_total_bits / base_bits) +
((int_total_bits % base_bits) ? 1 : 0);
const uint32_t last_radix_mask = int_mask_bits >>
((radix_num - 1) * base_bits);
int32_t shift = 0;
//Counting Sort
counter_type counting[max_bucket_symbols];
uint32_t* aux;
if (tmp_array == NULL)
aux = (uint32_t*)malloc_aligned(arrSize * sizeof(uint32_t));
else
aux = tmp_array;
uint32_t* in = _arr;
uint32_t* out = aux;
for (int32_t i = 0; i < radix_num; i++) {
// Cleaning counters
memset(counting, 0, sizeof(counter_type) * max_bucket_symbols);
// count the elements
for (uint32_t j = 0; j < arrSize; j++) {
uint32_t currItem = in[j];
uint32_t bucket_index = (((uint32_t)currItem >>
shift) & base_mask);//0xff
counting[bucket_index]++;
}
//compute offsets
counter_type acc = 0;
for (uint32_t j = 0; j < max_bucket_symbols; j++) {
counter_type tmp = counting[j];
counting[j] = acc;
acc += tmp;
}
// place elements in the output array
for (uint32_t j = 0; j < arrSize; j++) {
uint32_t currItem = in[j];
uint32_t bucket_index = (((uint32_t)currItem >>
shift) & base_mask);//0xff
counter_type out_index = counting[bucket_index];
counting[bucket_index]++;
out[out_index] = currItem;
}
//swap out, in
uint32_t* tmp = in;
in = out;
out = tmp;
// Change shift value for next iterations
shift += base_bits;
}
if (in != _arr)
memcpy(_arr, in, arrSize * sizeof(uint32_t));
if (tmp_array == NULL)
free_aligned(aux);
}
You can find the updated source code: here.
The sorting cost of this algorithm is O(4n) for 32-bit integers.
It is necessary to go through the input array 4 times to filter the 4 bytes of the integers that we are sorting.
Note: This algorithm does not use branch to sort the numbers!
4. Results
The implementations were compared:
- std::sort
- mergesort from the Cormen Algorithms book
- Out optimized radixsort
- Variation of the radixsort using multithreading
Tested on 2 CPUs:
- Intel Core i5-2415M
- freqüência: 2.3GHz
- núcleos/threads: 2/4
- cache
- L1: 64K (per core)
- L2: 256K (per core)
- L3: 3MB (shared)
- OS: MacOSX Catalina
- AMD Ryzen 7 5700X:
- freqüência: 3.4GHz a 4.6GHz
- núcleos/threads: 8/16
- cache
- L1: 64K (per core)
- L2: 512K (per core)
- L3: 32MB (shared)
- OS: Windows 11
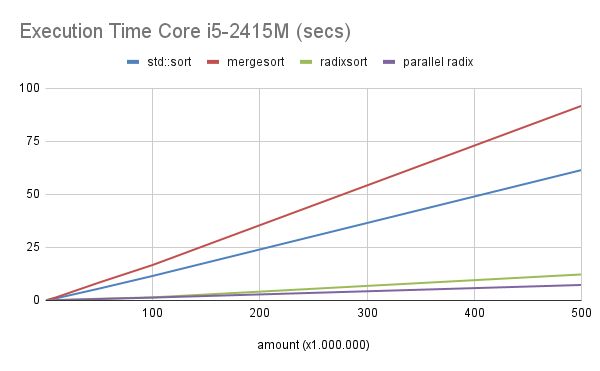
Execution Time Core i5-2415M (secs)
| amount (Mega) | std::sort | mergesort | radixsort | parallel radix |
|---|---|---|---|---|
| 0,1 | 0,00859 | 0,011625 | 0,001792 | 0,00314 |
| 0,5 | 0,047326 | 0,056289 | 0,008077 | 0,006643 |
| 1 | 0,094156 | 0,141766 | 0,016477 | 0,013934 |
| 5 | 0,496428 | 0,730969 | 0,097043 | 0,058909 |
| 10 | 1,002387 | 1,466769 | 0,190554 | 0,120432 |
| 50 | 5,577532 | 8,423516 | 0,819284 | 0,669023 |
| 100 | 11,55444 | 16,711819 | 1,453791 | 1,351016 |
| 500 | 61,453808 | 91,720573 | 12,25717 | 7,295864 |
On Core i5, comparing the single thread version with std::sort, the radixsort algorithm gets speedup around 5.
In the parallel version (parallel radix), compared to std::sort, the speedup is around 8. Except for the first case with 100,000 numbers, which was 2.7.
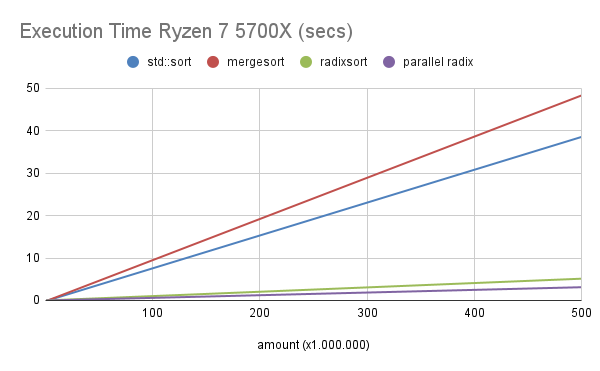
Execution Time Ryzen 7 5700X (secs)
| amount (Mega) | std::sort | mergesort | radixsort | parallel radix |
|---|---|---|---|---|
| 0,1 | 0,004388 | 0,006018 | 0,000999 | 0,000779 |
| 0,5 | 0,02543 | 0,033821 | 0,004812 | 0,002817 |
| 1 | 0,053115 | 0,070211 | 0,009914 | 0,005108 |
| 5 | 0,298237 | 0,385438 | 0,050997 | 0,0224 |
| 10 | 0,616527 | 0,800266 | 0,101511 | 0,04485 |
| 50 | 3,442063 | 4,321374 | 0,510289 | 0,228431 |
| 100 | 7,127363 | 8,943944 | 1,025262 | 0,581957 |
| 500 | 38,642517 | 48,442616 | 5,125806 | 3,129168 |
In Ryzen 7, comparing the single thread version with std::sort, the radixsort algorithm has speedup ranging from 4.4 to 7.5 in an increasing way according to the input size.
In the parallel version (parallel radix), compared to std::sort, the speedup ranges from 5.6 to 15.
See the graphics below:
5. Discussion of Results
In all tested systems, gains were observed using the radixsort algorithm, and with some optimization in the parallel version of it.
In the singlethread execution, the Ryzen 7 system presented a higher speedup due to its larger amount of L2 and L3 cache memory, in relation to the Core i5 system.
In the multithreaded execution, the Ryzen 7 system presented a higher speedup due to its larger number of cores/threads and also due to the larger amount of L2 and L3 cache memory, in relation to the Core i5 system.
6. Conclusion
One question that was raised is that since we do not use comparisons to sort the numbers, the CPU cost of this algorithm ends up being more the filtering operations of the radix sort (shift, and) and the count of the counting sort.
As bit ALU operations are generally the most optimized on a CPU (they spend less cycles), it makes me believe that another factor, not addressed in this post, that may be interfering in our times is the transfer speed of the memory bus, because the algorithm needs to loop through and write the input array 4 times to generate the final result.
This observation becomes feasible when we observe that Ryzen 7 speedups are higher than Core i5 speedups, both in single thread and in multi thread. Whereas one of the differences between the two is the amount of L2 and L3 cache memory.
This solution presented serves to sort only integer numbers. If you want to apply it to floating point numbers, you need to use the algorithm below to convert the binary representation of the same so that sorting still works:
static uint32_t sort_float_to_uint32(const float &_f) {
uint32_t f = *(uint32_t*)&_f;
uint32_t mask = (-int32_t(f >> 31)) | 0x80000000;
return f ^ mask;
}
For cases where a more complex comparison is needed for sorting, you should use another classical algorithm. In this case, the best complexity we usually have is O(n log n).
Hope you liked the content.
best regards,
Alessandro Ribeiro
